PCAS Expansion, Growth, Research, and SIGCSE 2024 Presentations

The ACM SIGCSE Technical Symposium is March 20-23 in Portland (see website here). I rarely blog these days, but the SIGCSE TS is a reminder to update y’all with what’s going on in the College of Literature, Science, & the Arts (LSA) Program in Computing for the Arts and Sciences (PCAS). PCAS is my main activity these days. Here’s the link to the PCAS website, which Tyrone Stewart and Kelly Campbell have done a great job creating and maintaining. (Check out our Instagram posts on the front page!)

PCAS Expansion

I’ve blogged about our first two courses, COMPFOR (COMPuting FOR) 111 “Computing’s Impact on Justice: From Text to the Web” and COMPFOR 121 “Computing for Creative Expression.” Now, we’re up to eight courses (see all the courses described here). As I mentioned at the start of PCAS, we think about computing in LSA in three themes: Computing for Discovery, Expression, and Justice. Several of these courses are collaborations with other departments, like our Discovery classes with Physics, Biophysics, Ecology and Evolutionary Biology, and Linguistics.

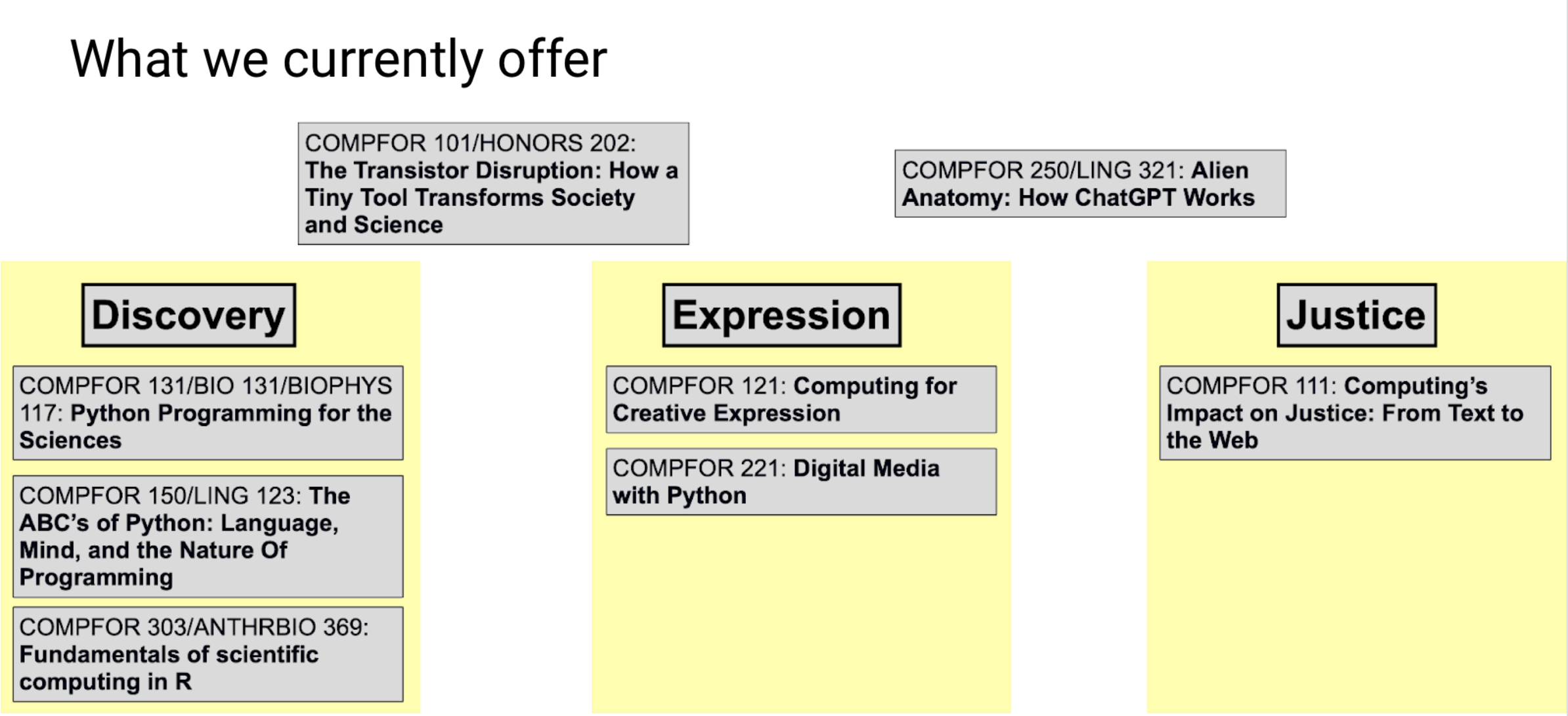
This semester, I’m teaching two brand new courses. That means that I’m creating them just ahead of the students. I did this in Fall 2022 for our first two courses (see links to the course pages here with a description of our participatory design process), and I hope to never do this again. It’s quite a sprint to always be generating material, all semester long, for about a hundred students.

One course is like the Media Computation course I developed at Georgia Tech, but in Python 3: COMPFOR 221: Digital Media with Python. The course title has changed. When we first offered it, we called it “Python Programming for Digital Media,” and at the end of registration, we had only five students enrolled! We sent out some surveys and found that we’d mis-named it. Students read “Python Programming” and skipped the rest. The class filled once we changed our messaging to emphasize Digital Media first.

When we taught Media Computation at Georgia Tech, we used Jython and our purpose-built IDE, JES. Today, there’s jes4py that provides the JES media API in Python 3. I had no idea how hard it was to install libraries in Python 3 today! I’m grateful to Ben Shapiro at U-W who helped me figure out a bunch of fixes for different installation problems (see our multi-page installation guide).

The second is more ambitious. It’s a course on Generative AI, with a particular focus on how it differs from human intelligence. We call it Alien Anatomy: How ChatGPT Works. It’s a special-topics course this semester, but in the future, it’ll be a 200-level (second year undergraduate) course with no pre-requisites open to all LSA students, so we’re relying on teaspoon languages and Snap! with a little Python. I’m team-teaching with Steve Abney, a computational linguist. Steve actually understands LLMs, and I knew very little. He’s been a patient teacher and a great partner on this. I’ve had to learn a lot, and we’re relying heavily on the great Generative AI Snap! projects that Jens Mönig has been creating, SciSnap from Eckart Modrow, and Ken Kahn’s blocks that provide an API to TensorFlow.

As of January, we are approved to offer two minors: Computing for Expression and Computing for Scientific Discovery. We have about a half dozen students enrolled so-far in the minors, which is pretty good for three months in.

PCAS Growth

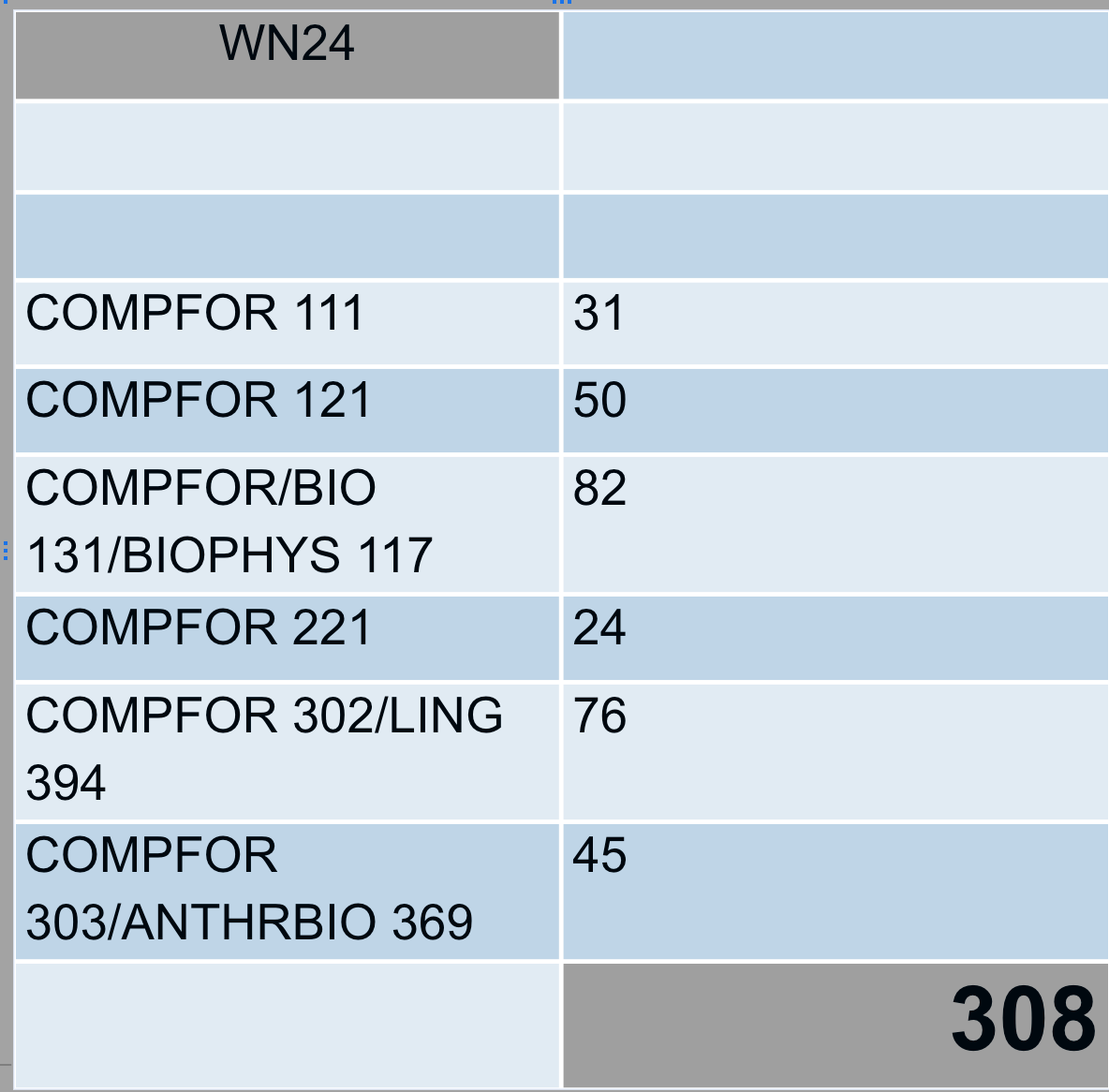
When I offered the first two courses in Fall 2022, we had 11 students in Expression and 14 in Justice. Now, we’re up to 308 students enrolled. That’s probably our biggest challenge — managing growth and figuring out how to sustain it.

Research in PCAS

We’re starting to publish some of what we’re learning from PCAS. Last November, Gus Evrard and I published a paper at the Koli Calling International Conference on Computing Education Research about the process that we followed co-chairing the LSA Computing Education Task Force to figure out what LSA needed in computing education. That paper, Identifying the Computing Education Needs of Liberal Arts and Sciences Students, won a Best Discussion Paper Award. Here’s Gus and me at the conference banquet when we got our award.

Tamara Nelson-Fromm just presented a paper at the 2024 PLATEAU Workshop on evidence we have suggesting transfer of learning from teaspoon languages into our custom Snap! blocks. I’ll wait until those papers are released to tell you more about that.

SIGCSE 2024 Presentations

We’re pretty busy at SIGCSE 2024, and almost all of our presentations are connected to PCAS.

Thursday morning, I’m on a panel led by Kate Lehman on “Re-Making CS Departments for Generation CS” 10:45 – 12:00 at Oregon Ballroom 203. This is going to be a hardball panel. Yes, we’ll talk about radical change, but be warned that Aman and I are on the far end of the spectrum. Aman is going to talk about burning down the current CS departments to start over. I’m going to talk about giving up on traditional CS departments ever addressing the needs of Generation CS (because they’re too busy doing something else) and that we need more new programs like PCAS. I’m looking forward to hear all the panelists — it’ll be a fun session.

Thursday just after lunch, Neil Brown and I are presenting our paper, Confidence vs Insight: Big and Rich Data in Computing Education Research 13:45 – 14:10 at Meeting Room D135. It’s an unusual computing education research paper because we’re making an argument, not offering an empirical study. We’re both annoyed at SIGCSE reviewers who ask for contextual information (Who were these students? What programming assignments were they working on? What was their school like?) from big (millions of points) data, and then complaining about small sample sizes from rich data with interviews, personal connections, and contextual information. In the paper, we make an argument about what are reasonable questions to ask about each kind of data. In the presentation, the gloves come off, and we show actual reviews. (There are also costumes.)

We don’t really get into why SIGCSE reviewers evaluate papers with criteria that don’t match the data, but I have a hypothesis. SIGCSE reviewers are almost all CS teachers, and they read a paper asking, “Does this impact how I teach? Does it tell me what I need to do in my class? Does it convince me to change?” Those questions are too short-sighted. We need papers that answer those questions to help us with our current problems, but we also need to have knowledge for the next set of problems (like when we start teaching entirely new groups of students). The right question for evaluating a computing education research paper is, “Does this tell the computing education research community (not you the reviewer, personally, based on your experience) something we didn’t know that’s worth knowing, maybe in the future?”

At the NSF Project Showcase Thursday 15:45 – 17:00 at Meeting Rooms E143-144, Tamara Nelson-Fromm is going to show where we are on our Discrete Mathematics project. She’ll demonstrate and share links to our ebooks for solving counting problems with Python and with one of our teaspoon languages, Counting Sheets.

In the “second flock” of Birds of a Feather sessions Thursday 18:30 – 19:20 at Meeting Room D136, we’re going to be a part of Zach Dodd’s group on “Computing as a University Graduation Requirement”. There’s a real movement towards building out computing courses for everyone, not just CS majors, as we’re doing in PCAS. Zach is pushing further, for a general education requirement. I’m excited for the session to hear what everyone is doing.

On Saturday afternoon 15:30 – 18:30 at Meeting Rooms B113, I’ll offer a three-hour workshop on how we teach in our PCAS courses for arts and humanities students, with teaspoon languages, custom Snap! blocks, and ebooks. Brian Miller has been teaching these courses this year, and he’s kindly letting me share the materials he’s been developing — he’s made some great improvements over what I did. This workshop was inspired by a comment from Joshua Paley in response to our initial posts about how we’re teaching, where he asked if I’d do a SIGCSE workshop on how we’re teaching PCAS. Will do it on Saturday!

How computing instructors plan to adapt to ChatGPT, GitHub Copilot, and other AI coding assistants (ICER 2023 paper): Guest blog post from Philip Guo

Hi everyone! This is Philip Guo from UC San Diego. My Ph.D. student (and soon-to-be faculty colleague) Sam Lau and I are presenting a paper at ICER 2023 on a topic that’s been at the top of many of our colleagues’ minds in recent months:

How are instructors planning to adapt their programming-related courses as more and more students start using AI coding assistance tools such as ChatGPT and GitHub Copilot?

A series of studies throughout 2021 and 2022 showed that GitHub Copilot can solve many kinds of CS1 and CS2 homework problems (see Section 3 of our paper for a summary of these studies). However, Copilot still requires users to install, configure, and activate it within an IDE like Visual Studio Code, which can be hard for novices to do. So when ChatGPT launched at the end of 2022, it made this AI technology far more accessible and easier to use. Now any student can visit the ChatGPT website, copy-paste in their homework assignments and instructor-provided starter code, and watch ChatGPT generate the solutions for them. Given this new reality we’re all now living in, Sam and I wanted to know what computing instructors are planning to do to ensure that their students are still learning well.

To gather a diverse sample of perspectives, we interviewed 20 university CS1/CS2 instructors across 9 countries (Australia, Botswana, Canada, Chile, China, Rwanda, Spain, Switzerland, United States) spanning all 6 populated continents. To our knowledge, our paper is the first empirical study to gather instructor perspectives about these AI coding tools that more and more students will likely have access to in the future.

Here’s a summary of our findings:

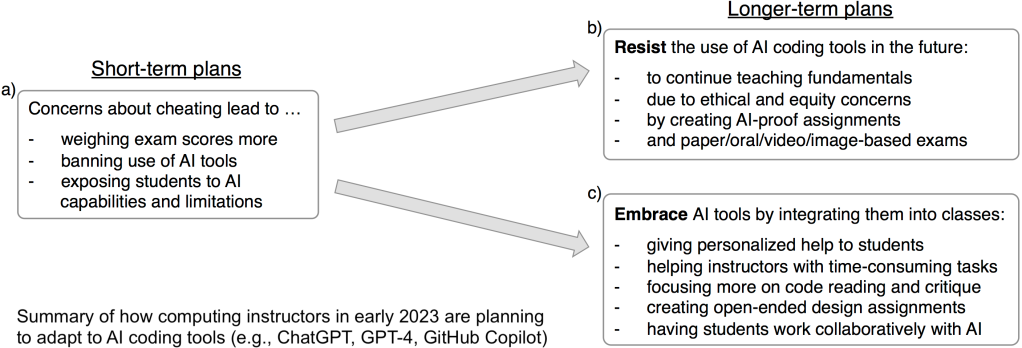
Short-term, many planned to take immediate measures to discourage AI-assisted cheating by weighing exams more, trying to ban these tools, or showing students their limitations. Then opinions diverged sharply about what to do longer-term, with one side wanting to resist AI tools by creating more AI-resistant assignments and exams, and the other side wanting to embrace these tools by integrating them deeply into introductory programming courses.

Our study findings capture a rare snapshot in time in early 2023 as computing instructors are just starting to form opinions about this fast-growing phenomenon but have not yet converged to any consensus about best practices. Using these findings as inspiration, we synthesized a diverse set of open research questions regarding how to develop, deploy, and evaluate AI coding tools for computing education. For instance, what mental models do novices form both about the code that AI generates and about how the AI works to produce that code? And how do those novice mental models compare to experts’ mental models of AI code generation? See Section 7 of our paper for more examples.

We hope that these findings, along with our open research questions, can spur conversations in our community about how to work with these tools in effective, equitable, and ethical ways. 

Check out our paper here and email us if you’d like to discuss anything related to it!

Sam Lau and Philip J. Guo. From “Ban It Till We Understand It” to “Resistance is Futile”: How University Programming Instructors Plan to Adapt as More Students Use AI Code Generation and Explanation Tools such as ChatGPT and GitHub Copilot. ACM Conference on International Computing Education Research (ICER), 2023.

The information won’t just sink in: Helping teachers provide technology-assisted data literacy instruction in social studies

Last year, Tammy Shreiner and I published an article in the British Journal of Educational Technology, “The information won’t just sink in: Helping teachers provide technology-assisted data literacy instruction in social studies.” (I haven’t been able to blog much the last year while starting up PCAS, so please excuse my tardiness in sharing this story.) The journal version of the paper is here, and our final submitted version (not paywalled) is available here.

Tammy and I used this paper to describe what happened (mostly during the pandemic) as we continued to provide support to in-service/practicing social studies teachers to adopt data literacy instruction in their classes. Since this was a journal on educational technology, we mostly focused on two technologies:

• The OER Tammy created to support data literacy in social studies education — see link here.
• DV4L, the Data Visualization for Learning tool that we created explicitly for social studies teachers — see link here.

When we started collaborating together, we looked for a theoretical model could inform our work. The end goal was easy to describe: we wanted social studies teachers to teach data literacy. But it’s hard to measure progress towards that big, high-level goal. Teachers are teaching data literacy, or they’re not. How do you know if you’re getting closer to the goal? We structured our work and our evaluation around the Technology Acceptance Model (TAM). TAM suggests that adoption of a new technology boils down to two questions: (1) is the technology actually useful in solving a problem that users care about, and (2) is the technology usable by the users? Those were things that we could measure progress towards.

During the pandemic, we ran several on-line professional learning opportunities — a workshop where practicing teachers could try out the OER with some guidance (e.g., “Make sure you see this” and “Why don’t you try that?”), and kick the tires on a bunch of tools including DV4L. We gathered lots of data on those teachers, and Tammy did the hard work of analyzing those data over time. We made progress on TAM goals — our tools got more usable and more useful.

But we still got very little adoption. TAM didn’t work for us. Adoption didn’t increase as usability and usefulness increased.

Why not? That’s a really big question, and we barely touch on it in this paper. It’s now a couple of years since we wrote the BJET article, and I could now tick off a dozen bullet points of reasons why teachers do not adopt, despite a technology being both useful and usable. I’m not going to list them here, because there are other publications in the pipeline. Bahare Naimipour, the EER PhD student working on our project, is finishing a case study of some teachers who did adopt and how their beliefs about data literacy changed.

I can give you a big meta-reason which probably isn’t a surprise to most education researchers but might be a surprise to many computer scientists: It’s not all about (or even mostly about) the technology. I led the group that worked on DV4L, and I’ve been directing students who have been helping Tammy make the OER more usable and useful (including build new tools that we haven’t yet released). TAM matters, but the characteristics of the individual teachers and the context of the teacher’s classroom are critical factors that technology is unlikely to overcome.

---

This is work funded in part by our National Science Foundation grant, #DRL2030919

New ICER paper award for Lasting Impact: Guest blog post from Quintin Cutts

I serve on the ACM SIGCSE International Computing Education Research (ICER) conference steering committee. Quintin Cutts is Chair of the Steering Committee. I offered to share his announcement of a new Lasting Impact paper award here in the blog.

This is an invitation to nominate a paper for the ICER Lasting Impact Award 2022, or to offer to serve on the judging panel.

Which ICER paper has caused you to change the way you teach, or the direction of your research?  Which has helped you to see and understand CS education more clearly?  Has it also had an impact right across the community?  I know which paper I would nominate, if I were allowed (but I’m not! – see below).  It’s been a game-changer for me, and across CS education.  Which one has done this for you and others?

1. Description of the award

The ICER Lasting Impact Award recognizes an outstanding paper published in the ICER Conference that has had meaningful impact on computing education. Significant impact can be demonstrated through citations, adoptions and/or adaptations of techniques and practices described in the paper by others, techniques described in the paper that have become widely recognized as best practices, further theoretical or empirical studies based on the original work, or other evidence the paper is an outstanding work in the domain of computing education research. The paper must have been published in ICER at least 10 years prior (i.e., for the 2022 award, papers must have been published in or before ICER 2011.)

2. Requirements for nominating a paper

a. An ACM Digital Library link to the paper being nominated.
b. A brief summary of the technical content of the paper and a brief explanation of its significance (limit 750 words).
c. Signatories to the summary and significance statement, with at least two current SIGCSE members. The name, contact email address and affiliation of each person who has agreed to sign the endorsement is acceptable.

3.  Nominating yourself as a potential award judge

Please consider nominating yourself as a potential judge. We are seeking judges who have significant experience in the ICER community. We will ask judges to serve who do not have nominated papers, to avoid conflicts of interest.

4. Additional Notes

a. ICER Steering Committee members cannot nominate papers.
b. The ICER Steering Committee chair, Quintin Cutts, will run the process this year, and his papers cannot be nominated.
c. In this inaugural year of the Award, we will not have a pre-defined rubric. We will ask the judges to report the rationale for their decision, and the report will be made public when we announce the winner.

5. Timetable (all times, 23.59 AoE)

17th July: Nominations close.
18th July: Judging panel selected from the candidate pool, depending on the number of nominations and conflicts. Papers sent out to the judges.
2nd August: Judging panel sits to deliberate and makes a decision, which is passed to PC chairs. Winner notified.

The award will be presented at the ICER 2022 conference in Lugano, Switzerland either in person or on-line.

6. Submitting nominations

Please send both paper nominations and judging self-nominations to me, Quintin Cutts at Quintin.Cutts@glasgow.ac.uk

Programming in blocks lets far more people code — but not like software engineers: Response to the Ofsted Report

A May 2022 report from the UK government Research Review Series: Computing makes some strong claims about block-based programming that I think are misleading. The report is summarizing studies from the computing education research literature. Here’s the paragraph that I’m critiquing:

Block-based programming languages can be useful in teaching programming, as they reduce the need to memorise syntax and are easier to use. However, these languages can encourage pupils to develop certain programming habits that are not always helpful. For example, small-scale research from 2011 highlighted 2 habits that ‘are at odds with the accepted practice of computer science’ (footnote). The first is that these languages encourage a bottom-up approach to programming, which focuses on the blocks of the language and not wider algorithm design. The second is that they may lead to a fine-grained approach to programming that does not use accepted programming constructs; for example, pupils avoiding ‘the use of the most important structures: conditional execution and bounded loops’. This is problematic for pupils in the early stages of learning to program, as they may carry these habits across to other programming languages.

I completely agree with the first sentence — there are benefits to using block-based programming in terms of reducing the need to memorize syntax and increasing usability. There is also evidence that secondary school students learn computing better in block-based programming than in text-based programming (see blog post). Blanchard, Gardner-McCune, and Anthony found (a Best Paper awardee from SIGCSE 2020) that university students learned better when they used both blocks and text than when they used blocks alone.

The two critiques of block-based programming in the paragraph are:

• “These languages encourage a bottom-up approach to programming, which focuses on the blocks of the language and not wider algorithm design.”
• “They may lead to a fine-grained approach to programming that does not use accepted programming constructs…conditional execution and bounded loops.”
  

Key Point #1: Block-based programming doesn’t cause either of those critiques. What about programming with blocks rather than text could cause either of these to be true?

I’m programming a lot in Snap! these days for two new introductory computing courses I’m developing at the University of Michigan. I’ve been enjoying the experience. I don’t think that either of these critiques are true about my code or that of the students helping me develop the courses. I regularly do top-down programming where I define high-level custom blocks, as I design my program overall. Not only do I use conditional execution and bounded loops regularly, but Snap allows me to create new kinds of control structures, which has been a terrific help as I create block-based versions of our Teaspoon languages. My experience is only evidence that those two statements need not be true, just because the language is block-based.

I completely believe that the studies being cited in this research report saw and accurately describe exactly these points — that students worked bottom-up and that they rarely used conditioned execution and bounded loops. I’m not questioning the studies. I’m questioning the inference. I don’t believe at all that those are caused by block-based languages.

Key Point #2: Block-Based Programming is Scaffolding, but not Instant Expertise. For those not familiar, here are two education research terms that will be useful in making my argument.

• Scaffolding is the support provided by a learner to enable them to achieve some task or process which they might not be able to achieve without that support. A kid can’t hop a fence by themselves, but they can with a boost — that’s a kind of scaffolding. Block-based programming languages are a kind of scaffolding (and here’s a nice paper from Weintrop and Wilensky describing how it is scaffolding — thanks to Ben Shapiro for pointing it out).
• The Zone of Proximal Development (ZPD) describes the difference between what a student can do on their own (one edge of the ZPD) and what they might be able to do with the support of a teacher or scaffolding (the far edge of the ZPD). Maybe you can’t code a linked list traversal on your own, but if I give you the pseudocode or give you a lecture on how to do it, then you can. But the far edge of ZPD is unlikely to be that you’re a data structure expert.

Let’s call the task that students were facing in the studies reviewed in the report: “Building a program using good design and with conditioned execution.” If we asked students to achieve this task in a text-based language, we would be asking them to perform the task without scaffolding. Here’s what I would expect:

• Fewer students would complete the task. Not everyone can achieve the goal without scaffolding.
• Those students who do complete the task likely already have a strong background in math or computing. They are probably more likely to use good design and to use conditioned execution. The average performance in the text-based condition would be higher than in the block-based condition — simply because you’ve filtered out everyone who doesn’t have the prior background..

Fewer people succeed. More people drop-out. Pretty common CS Ed result. If you just compare performance text vs. blocks, text looks better. For a full picture, you also have to look at who got left out.

So let’s go back to the actual studies. Why didn’t we see good design in students’ block-based programs? Because the far edge of the ZPD is not necessarily expert practice. Without scaffolding (block-based programming languages), many students are not able to succeed at all. Giving them the scaffolding doesn’t make them experts. The scaffolding can take them as far as the ZPD allows. It may take more learning experiences before we can get to good design and conditioned execution — if that even makes sense.

Key Point #3: Good software engineering practice is the wrong goal. Is “building a program using good design and with conditioned execution” really the task that students were engaging in? Is that what we want student to succeed at? Not everyone who learns to program is going to be a software engineer. (See the work I cite often on “alternative endpoints.”) Using good software engineering practices as the measure of success doesn’t make sense, as Ben Shapiro wrote about these kinds of studies several years ago on Twitter (see his commentary here, shared with his permission). A much more diverse audience of students are using block-based programming than ever used text-based programming. They are going to solve different problems for different purposes in different ways (a point I made in this blog post several years ago). Few US teachers in K-12 are taught how to teach good software engineering practice — that’s simply not their goal (a point that Aman Yadav made to me when discussing this post). We know from many empirical studies that most Scratch programs are telling a story. Why would you need algorithmic design and conditioned execution for that task? They’re not doing complicated coding, but the little bit of coding that they’re using is powerful and is engaging for students — and relatively few students are getting that. I’m far more concerned about the inequitable access to computing education than I am about whether students are becoming good software engineers.

Summary: It’s inaccurate to suggest that block-based programming causes bad programming habits. Block-based programming makes programming far more accessible than it ever has been before. Of course, we’re not going to see expert practice as used in text-based languages for traditional tasks. These are diverse novices using a different kind of notation for novel tasks. Let’s encourage the learning and engagement appropriate for each student.

Getting feedback on Teaspoon Languages from CS educators and researchers at the Raspberry Pi Foundation seminar series

In May, I had the wonderful opportunity to speak at the Raspberry Pi Foundation Seminar series. I’ve attended some of these seminars before. I highly recommend them (see past seminars here). It’s a terrific format. The speaker presents for up to a half hour, then everyone gets put into a breakout room for small group discussions. The participants and speaker come back for 30-35 minutes of intensive Q&A — at least, it feels “intensive” from the speaker’s perspective. The questions you get have been vetted through the breakout room process. They’re insightful, and sometimes critical, but always in a constructive way. I was excited about this opportunity because I wanted to make it a hands-on session where the CS teachers and researchers who attended might actually use some Teaspoon Languages and give me feedback on them. I have rarely had the opportunity to work with CS teachers, so I was excited for the opportunity.

Sue Sentance wrote up a very nice blog post describing my talk (thank you!) — see here. The video of the talk and discussion is available. You can watch the whole thing, or, you can read the blog post then skip ahead to where the conversation takes place (around 26:00 in the video). If you have been wondering, “Why isn’t Mark just using Logo, Scratch, Snap, or NetLogo? We already have great tools! Why invent new languages that are clearly less powerful than what we already have?”, then you should jump to 34:38 and see Ken Kahn (inventor of ToonTalk) push me on this point.

The whole experience was terrific for me, and I hope that it’s valuable for the viewer and attendees as well. The questions and comments indicated understanding and appreciation for what I’m trying to do, and the concerns and criticisms are valuable input for me and my team. Thanks to Sue, Diana Kirby, the Raspberry Pi Foundation, and all the attendees!

Three types of computing education research: for CS, for CS but not professionally, and for everyone

In February, I was invited to give a lecture at the University of Washington’s Allen School. I had a great day visiting there, even though it was all on Zoom. My talk is available on YouTube:

I got a chance to talk to Jeff Heer and Amy Ko before my visit. The U-W CSE department had been thinking about making a push into computing education research. They suggested that I describe the lay of the land — and particularly, to identify where I fit in that space. What I do these days (e.g. Teaspoon languages for history and mathematics classes) isn’t in the mainstream of computing education research, and it was important to tell people unfamiliar with the field, “There’s a lot more out there, and most of it doesn’t look like this.”

CS Education research dates back to the late 1960’s (see the history chapter that Ben du Boulay and I wrote). ACM SIGCSE started in 1968 with a particular focus on how to teach Computer Science and Information Technology majors. Much of what SIGCSE has published is focused even more specifically on the first course, which we now call CS1. This is a big and important space. These majors will be significant drivers of the world’s infrastructure.

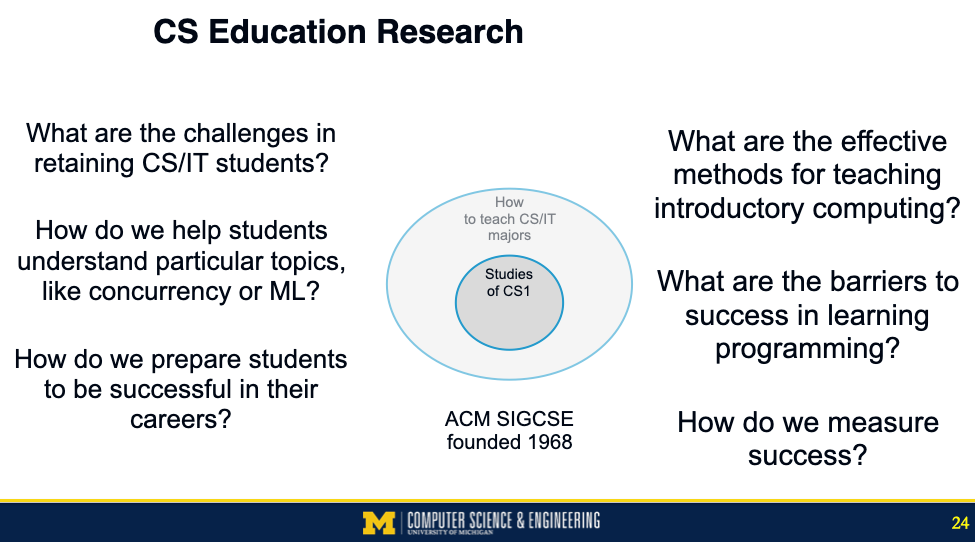
There is a growing trend in computing education research to look at people who are learning programming (like in the first circles), but not for the purpose of becoming technology professionals. This includes K-12 CS teachers, end-user programmers, and conversational programmers. This kind of research sometimes appears in venues like CHI, CSCW, and VL/HCC, and occasionally in venues like SIGCSE, RESPECT, and ITiCSE. These circles aren’t scaled correctly by size of potential student population. By most measures, the outer circle (of people learning programming but who aren’t going to become technology professionals) is at least ten times the size of the student population inside the first circles.

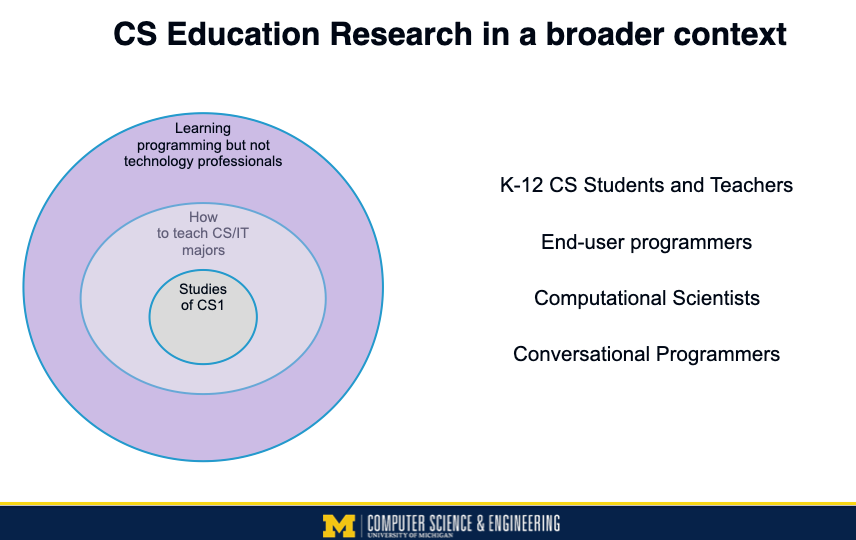
My research is one level further out. I’m interested in studying what should we be teaching to everyone, whether or not they’re going to program like professionals, and how do we facilitate that learning. These students might not use the same tools or languages, and certainly have different goals for studying computing. I offer three reasons for the broader “everyone” to learn computing (drawn from the work of C.P. Snow, Alan Perlis, Peter Naur, and Seymour Papert — see this earlier blog post):

• To make sure that technology is controlled by a democracy.
• To support new ways of thinking and learning.
• To be part of a new computational literacy, a new tool for human expression.

This outer circle is far bigger in terms of number of students potentially impacted than any of the inner circles. But it’s also where we know the least in terms of research results.

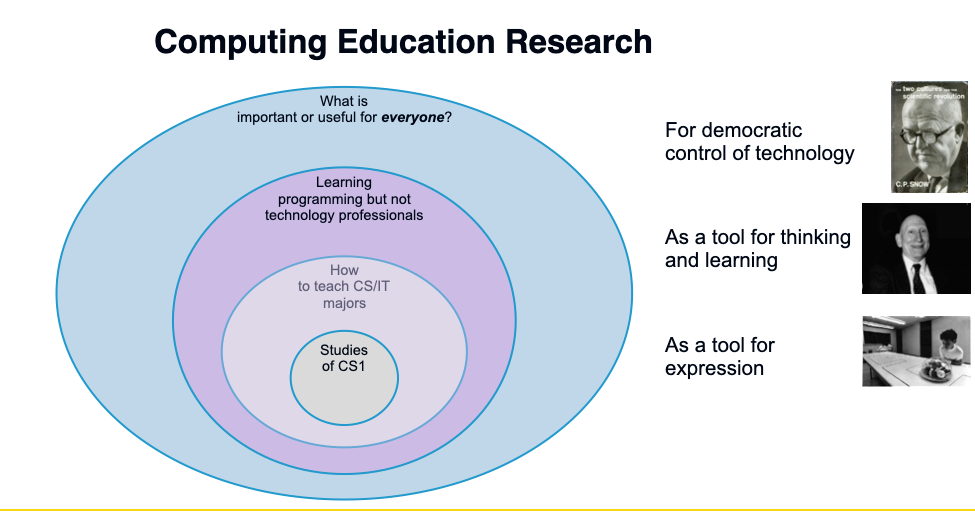
Take a look at the talk for more on this way of thinking about the field, and how I connect that to existing research. I’d be interested in your perspective on this framing.

Updates: NSF Funding to Study Learning with Teaspoon Languages for Discrete Mathematics

A few months before the pandemic started, Dr. Elise Lockwood at Oregon State reached out to me. She’d heard that I was interested in programming for teaching non-CS subjects, and that’s what she was doing. I loved what she was doing, and we started having regular chats.

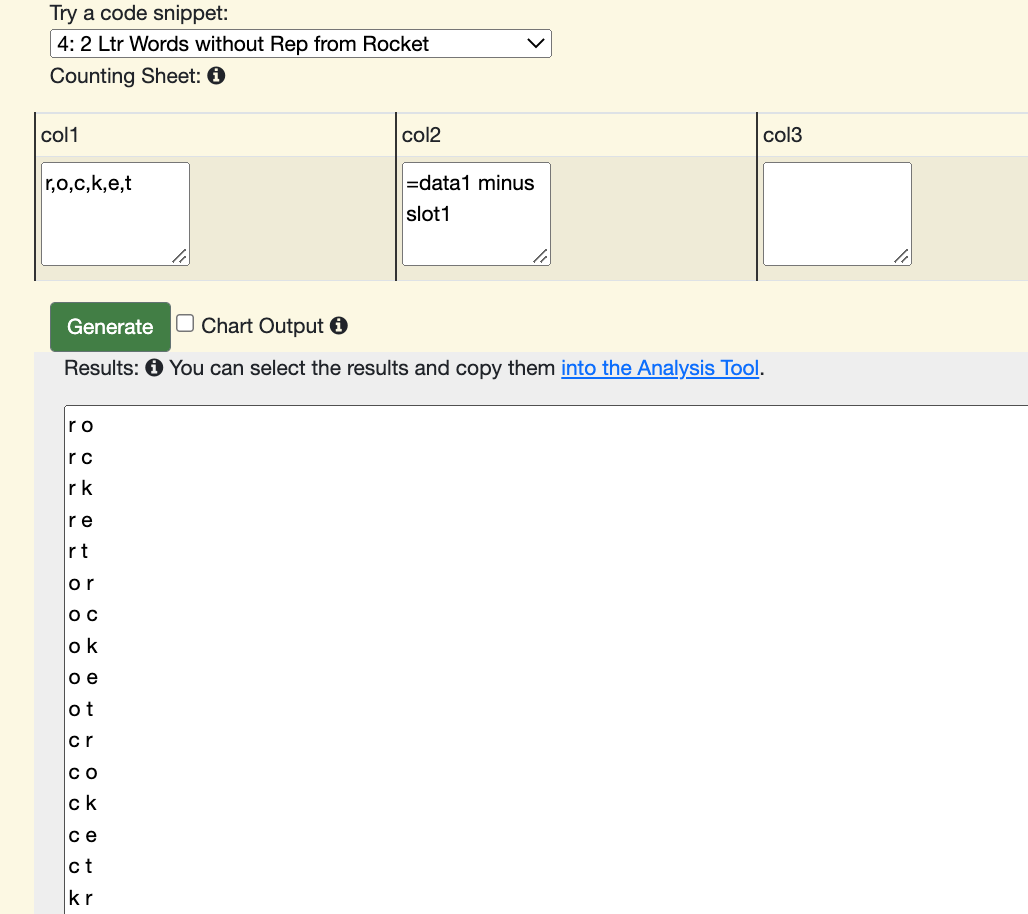
Elise is a mathematics education researcher who has been studying how students come to understand counting problems. Like “If you have three letters and four digits, how many license plates can you make?” Or “How many two letter words can you make from the letters ROCKET, if you don’t allow double letters?” She’s been exploring having students learn counting problems by manipulating Python programs to generate all the possible combinations, then counting them. (Check out her recent papers on her Google Scholar page, especially those with her student Adaline De Chenne.)

As I said, I loved what she was doing, but Python seemed heavy-handed for this. I was starting to work on our Teaspoon languages. Could we build lighter-weight languages for the same problems?

As I kept reading Elise’s papers, I started working on two possible designs.

In one of them (called Counting Sheets), we play off of students’ understanding of spreadsheets. You can just describe what you want in each column, and the system will exhaustively generate every combination:

Or you can use an “=“ formula that knows how to do very simple operations with sets. Here’s a solution to the two letter words from ROCKET without repeating problem:

This is one of the tools that we’ve been building in support for both Spanish and English keywords (like Pixel Equations, that I talked about last September):

Elise found Counting Sheets intriguing, but she was worried if it would work to make the iterative structures implicit and declarative. Would students need to see the iteration to be able to reason about the counting processes?

So, I built a second Teaspoon language, called Programmed Counting. Here, the loops are explicit, like Python, but the only variable type is a set, and the words and phrases of the language come from counting problems.

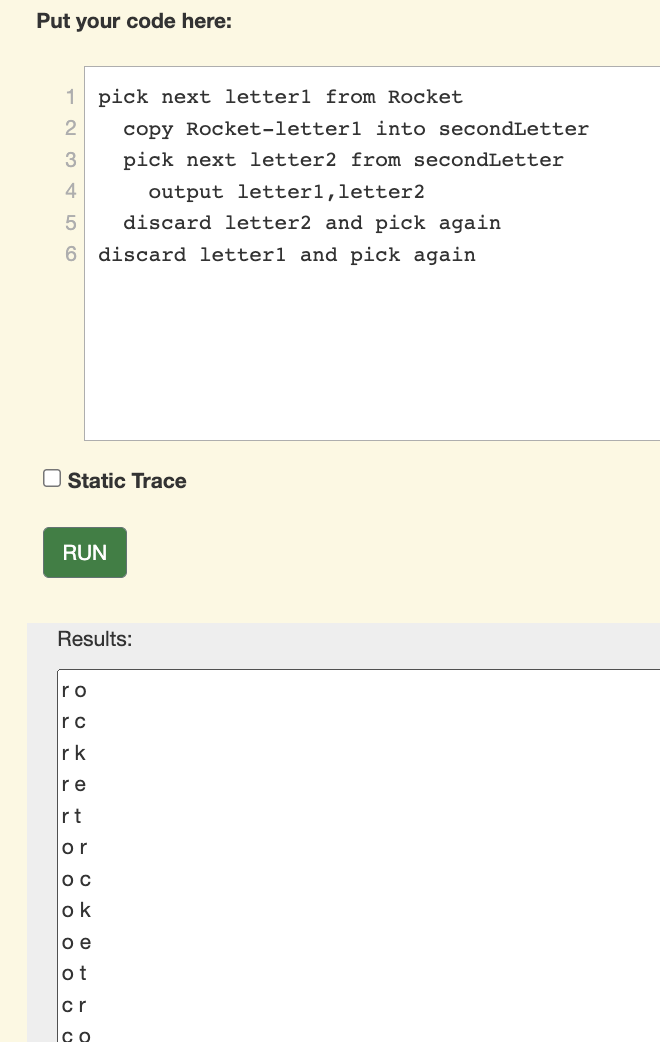
Elise was a real sport, trying out the languages as I generated prototypes and finding the holes in what I was doing. We met face-to-face only once, when I went to Portland for SIGCSE 2020 — the one that got cancelled the very morning it was supposed to start. I had lunch with Elise, and we worked for a few hours on the designs. Barb and I went home the next day, and the big pandemic lockdown started right afterwards.

Will these work for learning? We don’t know — but we just got funding from NSF to find out! “We” here is me and PhD student Emma Dodoo, and we’ll be involving Adaline as a consultant. Elise is currently a rotator at NSF, so she’s involved only from the sidelines because of NSF COI issues. Our plan is to run experiments with various combinations of the Teaspoon languages (one or both), standalone and with Python. Do we need Python if we have the Teaspoon languages? Do the Teaspoon languages serve as scaffolding to introduce concepts before starting into Python?

Below is the abstract on the new IUSE grant, as an overview of the project. University of Michigan CSE Communications wrote a nice article about the work, available here. Huge thanks to Jessie Houghton, Angela Li, and Derrick White who turned my LiveCode prototypes into functioning Web versions.

Abstract for NSF

Programming is a powerful tool that scientists, engineers, and mathematicians use to gain insight into their problems. Educators have shown how programming integrated into other subjects can be a powerful tool to enhance learning, from algebra to language arts. However, the cost is learning the programming language. Few students in the US learn programming — less than 5% of high school students nationwide. Most students do not have the opportunity to use programming to support ™ learning. This project is investigating a new approach to designing and implementing programming languages in classrooms: Task-specific programming (TSP) languages. TSP languages are explicitly design for integration in specific classes, to meet teacher needs, and to be usable with less than 10 minutes of instruction. TSP languages can make the power of programming to enhance learning more accessible. This project will test the value of TSP languages in discrete mathematics, which is a gateway course in some computer science programs.

The proposed project tests the use of two different TSP languages and contrasting that with a traditional programming language, Python. The proposed work will contribute to understanding about (1) the role of programming in learning in discrete mathematics, (2) the value of task-specific languages to scaffold learning, (3) how alternative representational forms for programming influence student use of TSP languages, and (4) how the use of TSP languages alone or in combination with traditional languages enhance students’ sense of authenticity and ability to transfer knowledge.

Helping social studies teachers to teach data literacy with Teaspoon languages

Last year, Tammy Shreiner and I received NSF funding to develop and evaluate computational supports for helping social studies teachers to teach data literacy and computing(see post here). We’re excited about what we’re doing and what we’re learning. Here’s an update on where we’re at on the project.

Teaspoon Languages

We have a chapter in the new book by Aman Yadav and Ulf Dalvad Berthelsen Computational Thinking in Education: A Pedagogical Perspective. This is the publication where we introduce the idea of Teaspoon Languages. Teaspoon languages are a form of task-specific languages (TSP => Teaspoon — see?). Teaspoon languages:

• Support learning tasks that teachers (typically non-CS teachers) want students to achieve;
• Are programming languages, in that they specify computational processes for a computational agent to execute; and
• Are learnable in less than 10 minutes, so that they can be learned and used in a one hour lesson. If the language is never used again, it wasn’t a significant learning cost and still provided the benefit of a computational lesson.
  

We say that we’re adding a teaspoon of computing to other subjects. The goal is to address the goal of “CS for All” by integrating computing into other subjects, by placing the non-CS subjects first. We believe that programming can be useful in learning other subjects. Our primary goal is to meet learning objectives outside of CS using programming. Teachers (and students eventually) will be learning foundational CS content — but not necessarily the content we typically teach in CS classes. All students should learn that a program is non-WYSIWYG, that it’s a specification of a computational process that gets interpreted by a computational agent, that programming languages can be in many forms, and that all students can be successful at programming.

Our chapter, “Integrating Computing through Task-Specific Programming for Disciplinary Relevance: Considerations and Examples” (see link here) offers two use cases of how we imagine teaspoon languages to work in classrooms (history and language arts in these examples). The first use case is around DV4L, our Data Visualization for Learning tool. The second is around a chatbot language that we developed —- and have long since discarded.

We develop our teaspoon languages in a participatory design process, where teachers try our prototypes in authentic tasks as design probes, and then they tell us what we got wrong and what they really want. Our current iteration is called Charla-bots and is notable for having user-definable languages. We have a variety of Charla-bot languages now, with English, Spanish, and mixed keywords.

Our vision for teaspoon languages is a contrast with the “Hour of Code” approach. The “Hour of Code” is a one hour programming activity that many schools use in every grade, typically once a year during CS Ed Week (in early December). The great idea is to build familiarity and confidence in programming by showing students real computer science every year. The teaspoon languages approach is to imagine one or two little learning programming activity in every social studies, language arts, and mathematics class every year. Each of these languages is tiny and different. The goal is that by the time that US students take a CS class (typically, in high school or undergraduate), they will have had many programming experiences, have seen a variety of types of programming languages, and have a sense that “programming isn’t hard.”

Meeting the Needs of Social Studies Teachers

The second paper, “Using Participatory Design Research to Support the Teaching and Learning of Data Literacy in Social Studies” (see link here) was just presented in October by Tammy at CUFA, the College and University Faculty Assembly 2021 of the National Council of the Social Studies. (We have a longer form of this paper that we have just submitted to a journal.) This is an exciting paper for me because it’s exactly addressing the critical challenge in our work. We can design and implement all kinds of prototype Teaspoon languages, but to achieve our goals, teachers in disciplines other than CS have to see value and adopt them.

The paper is about our workshops with practicing social studies teachers. Tammy has a goal to teach social studies teachers how to teach data literacy. She has built a large online education resource (OER) on teaching data literacy in social studies. Learning data literacy involves being able to read, comprehend, and argue with data visualizations, but also being able to create them. That’s where we come in. Her OER links to several tools for creating data visualizations, like Timeline JS, CODAP, and GapMinder. Most of them were not created for social studies teachers or classes. When we run these workshops, our tools are just in-the-mix. We offer scaffolding for using all of them. These are our design probes. The teachers use the tools and then tell us what they really want. These are our data, and we analyze them in detail —- as in this paper.

Let’s jump to the bottom line: We’re not there yet. The teachers love the OER, but get confused about why should do in their classes. They find the tools for data visualization fascinating, but overwhelming. They like DV4L a lot:

One pre-service teacher explained that they preferred our prototype over other tools because “(with the prototype DV4L) I found myself asking questions connected to the data itself, rather than asking questions in order to figure out how to work the visual.”

Recently, I held a focus group with some social studies teachers who told me that they won’t use any computational tools —- they believe in teaching data visualization, but all created with pencil and ruler. That’s our challenge: Can we be more powerful, more enticing, and easy enough to beat out pencil and ruler? Our tool, DV4L, is purpose-built for these teachers, and they appreciate its advantages — and yet, few are adopting. That’s where we need to work next.

Opportunities for Social Studies Teachers to Get Involved

If you know a social studies teacher who would want to keep informed about our work and perhaps participate in our workshops or studies, please have them sign up on our mailing list. Thank you!

Often, what teachers tell us they really want suggests new features or entirely new tools. We have two ongoing studies where we are looking for design feedback from social studies teachers. If you know social studies teachers who would like to play with something new (and we’ll pay them for their time), would you please forward these to them?

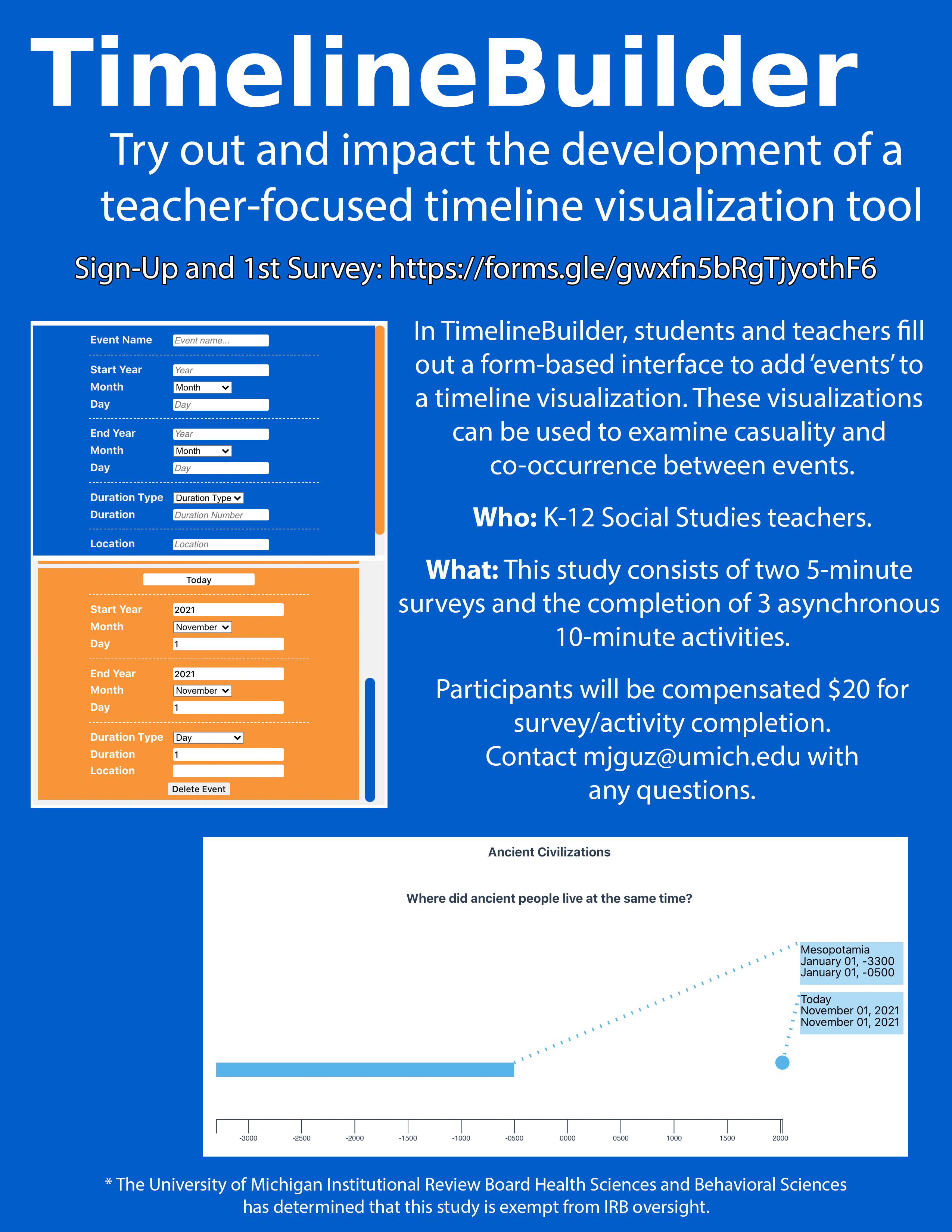
Timeline Builder

We’re looking for K-12 Social Studies teachers to try out our new timeline visualization tool, TimelineBuilder. TimelineBuilder has been made with teachers and usability in mind. In it, ‘events’ are added to a timeline using a form-based interface. Changes to the timeline can be seen automatically, with events showing up as soon as they are added.

This study will consist of completing 2 surveys and 3 asynchronous activities guided by worksheets. All participants will be compensated with a $20 gift card for survey and activity completion. There is an additional option to be invited to a focus group, which will provide additional compensation.

If you are interested in participating in this study, you can complete the consent form and 1st survey here. (Plain text Link: https://forms.gle/gwxfn5bRgTjyothF6 )

Please contact Mark Guzdial (mjguz@umich.edu) or Tamara Nelson-Fromm (tamaranf@umich.edu) with any questions.

The University of Michigan Institutional Review Board Health Sciences and Behavioral Sciences has determined that this study is exempt from IRB oversight.

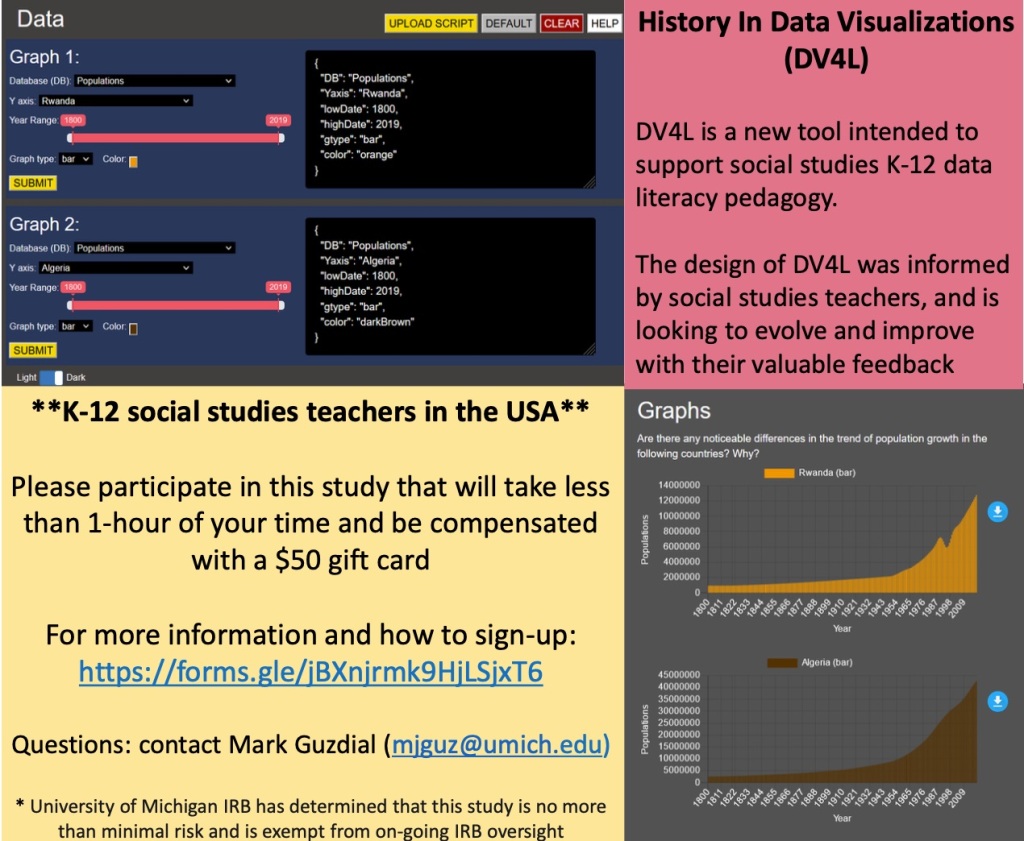
DV4L Scripting Study

Through our work with social studies educators thus far, we have designed the tools DV4L-Basic and DV4L-Scripting specifically to support data literacy standards in social studies classrooms. If you are a social studies middle or high school teacher, we would love to hear your feedback. If you can spare less than an hour of your time to participate in our study, we will send you a $50 gift card for your time and valuable feedback.

If you are interested but want more details, please visit/complete the consent form here: https://forms.gle/yo3yWGThQ1wnhu7g7

For questions or concerns, please contact Mark Guzdial (mjguz@umich.edu) or Bahare Naimipour (baharen@umich.edu).

References

Guzdial, M. and Tamara L. Shreiner. 2021. “Integrating Computing through Task-Specific Programming for Disciplinary Relevance: Considerations and Examples.” In Computational Thinking in Education: A Pedagogical Perspective, Aman Yadav and Ulf Dalvad Berthelsen (Eds). PDF of Submitted.

Shreiner, Tamara L., Mark Guzdial, and Bahare Naimipour. 2021. “Using Participatory Design Research to Support the Teaching and Learning of Data Literacy in Social Studies.” Presented at CUFA, the College and University Faculty Assembly 2021 of the National Council of the Social Studies. PDF

Media Computation today: Runestone, Snap!, Python 3, and a Teaspoon Language

I don’t get to teach Media Computation¹ since I moved to the University of Michigan, so I haven’t done as much development on the curriculum and infrastructure as I might like if I were teaching it today. I did get a new version of JES (Jython Environment for Students) released in March 2020 (blog post here), but have rarely even started JES since then.

But using Jython for Media Computation is so 2002. Where is Media Computation going today?

I’ve written a couple of blog posts about where Media Computation is showing up outside of JES and undergraduate CS. Jens Moenig has been doing amazing things with doing Media Computation in Snap! — see this blog post from last year on his Snap!Con keynote talk. SAP is now offering a course From Media Computation to Data Science using Snap! (see link here). Barbara Ericson’s work with Runestone ebooks (see an example blog post here) includes image manipulation in Python inside the browser at an AP CS Principles level (see example here). The amazing CS Awesome ebook that Beryl Hoffman and Jen Rosato have been doing with Barb for AP CS A includes in-browser coding of Java for the Picture Lab (see example here).

I was contacted this last January by Russ Tuck and Jonathan Senning. They’re at Gordon College where they teach Media Computation, but they wanted to do it in Python 3 instead of Jython. You can find it here. It works SO well! I miss having the image and sound explorers, but my basic demos with both images and sounds work exactly as-is, with no code changes. Bravo to the Gordon College team!

Most of my research these days is grounded in Task-Specific Programming languages, which I’ve blogged about here (here’s a thread of examples here and here’s an announcement of funding for the work in social studies). We now refer to the project as Teaspoon Computing or Teaspoon Languages — task-specific programming => TSP => Teaspoon. We’re adding a teaspoon of computing into other subjects. Tammy Shreiner and I have contributed a chapter on Teaspoon computing to a new book by Aman Yadav and Ulf Dalvad Berthelsen (see announcement of the book here).

We have a new Teaspoon language, Pixel Equations, that uses Media Computation to support an Engineering course in a Detroit Public School. Here, students choose a picture as input, then (1) enter the boolean equations for what pixels to select and (2) enter equations for new red, green, and blue values for those pixels. The conditionals and pixel loops are now implicit.

In several of our tools, we’re now exploring bilingual or multilingual interfaces, inspired by Sara Vogel’s work on translanguaging (see paper here) and Manuel Pérez-Quiñones’s recent work on providing interfaces for bilingual users (see his TED talk here and his ACM Interactions paper here). You can see in the screenshot below that colors can be referenced in either English or Spanish names. We’re now running participatory design sessions with teachers using Pixel Equations.

I’m planning a series of blog posts on all our Teaspoon languages work, but it’ll take a while until I get there.

---

1. For new readers, Media Computation is a way of introducing computing by focusing on data abstractions used in digital media. Students write programs to manipulate pixels of a picture (to create photo filters), samples of a sound (e.g., to reverse sounds), characters of a text, and frames of a video (for video special effects). More at http://mediacomputation.org ↩

ICER 2021 Preview: The Challenges of Validated Assessments, Developing Rich Conceptualizations, and Understanding Interest #icer2021

The International Computing Education Research Conference (ICER) 2021 is this week (website here). It should have been in Charleston, South Carolina (one of my favorite cities), but it will instead be all on-line. Unlike previous years, if you are not already registered, you’re unfortunately out of luck. As seen in Matthias Hauswirth’s terrific guest blog post from last week (see here), getting set up in Clowdr is complicated. ICER won’t have the resources to bring people on-line and get them through the half hour prep sessions on-the-fly. There will be no “onsite” registration.

However, all the papers should be available in the ACM Digital Library (free for some time), and I think all the videos of the talks will be made available after the fact, so you can still gain a lot from the conference. Let me point out a few of the highlights that I’m excited about. (As of this writing, the papers are not yet appearing in the ACM DL — all the DOI links are failing for me. I’ll include the links here in hopes that everything is fixed soon.)

Our keynoter is Tammy Clegg, whom I got to know when she was a PhD student at Georgia Tech. She’s now at U. Maryland doing amazing work around computation and relevant science learning. I’m so looking forward to hearing what she has to say to the ICER community.

Miranda Parker, Allison Elliott Tew, and I have a paper “Uses, Revisions, and the Future of Validated Assessments in Computing Education: A Case Study of the FCS1 and SCS1.” This is a paper that we planned to write when Miranda first developed the SCS1 (first published in 2016). We created the SCS1 in order to send it out to the world for use in research. We hoped that we could sometime later do in CS what Richard Hake did in Physics, when he used the FCI to make some strong statements about teaching practices with a pool of 6,000 students (see paper here). Hake’s paper had a huge impact, as it started making the case to shift from lecture to active learning. Could we use the collected use of the SCS1 to make some strong arguments for improving CS learning? We decided that we couldn’t. The FCI was used in pretty comparable situations, and it’s tightly focused on force. CS1 is far too broad, and FCS1 and SCS1 are being used in so many different places — not all of which it’s been validated for. Our retrospective paper is kind of a systemic literature review, but it’s done from the perspective of tracing these two instruments and how they’ve been used by the research community.

One of the papers that I got a sneak peek at was “When Wrong is Right: The Instructional Power of Multiple Conceptions” by Lauren Margulieux, Paul Denny, Katie Cunningham, Mike Deutsch, and Ben Shapiro. The paper is exploring the tensions between direct instruction and more student-directed approaches (like constructionism and inquiry learning) (see a piece I did in 2015 about these tensions). The basic argument of this new paper is that just telling students the right answer is not enough to develop rich understanding. We have to figure out how to help students to be able to hold and compare multiple conceptions (not all of which is canonical or held by experts), so that they can compare and contrast, and use the right one at the right time.

I’m chair for a session on interest. While I haven’t seen the papers yet, I got to watch the presentations (which are already loaded in Clowdr). “Children’s Implicit and Explicit Stereotypes on the Gender, Social Skills, and Interests of a Computer Scientist” by de Wit, Hermans, and Aivaloglou is a report on a really interesting experiment. They look at how kids associate gender with activities (e.g., are boys more connected to video games than girls?). The innovative part is that they asked the questions and timed the answers. A quick answer likely connects to implicit beliefs. If they take a long time to answer, maybe they told you what they thought you wanted to hear? The second paper “All the Pieces Matter: The Relationship of Momentary Self-efficacy and Affective Experiences with CS1 Achievement and Interest in Computing” by Lishinski and Rosenberg asks about what leads to students succeeding and wanting to continue in computing. They look at students affective state coming into CS1 (e..g, how much do they like computing? How much do they think that they can succeed in computing?), and relate that to students’ experiences and affective state after the class. They make some interesting claims about gender — that gender gaps are really self-efficacy gaps.

One of the more unusual sessions is a pair of papers from IT University of Copenhagen that make up a whole session. ICER doesn’t often give over a whole session to a single research group on multiple papers. One is “Computing Educational Activities Involving People Rather Than Things Appeal More to Women (Recruitment Perspective)” and the other is “Computing Educational Activities Involving People Rather Than Things Appeal More to Women (CS1 Appeal Perspective).” The pitch is that framing CS1 as being about people rather than things leads to better recruitment (first paper) and more success in CS1 (second paper) in terms of gender diversity. It’s empirical support for a hypothesis that we’ve heard before, and the authors frame the direction succinctly: “CS is about people not things.” Is that succinct enough to get CS faculty to adopt this and teach CS differently?

The Drawbacks of the One-Second Conference Trip. Or, how to prepare for ICER 2021. Guest Blog Post from Matthias Hauswirth

I miss physical conferences. But there are some things about them I do not miss at all. I don’t miss sprinting through airports to catch a connecting flight. I don’t miss standing in line at immigration for over an hour, just to enter the next long line to get through customs. And I don’t miss sitting in a tight middle seat for ten hours straight.

With today’s virtual conferences the trips are more pleasant. I can travel there with a single mouse click. It’s a one-second trip. And I love that! *

However, by eliminating the trip to the conference, we also eliminated an opportunity to prepare for the conference while being stuck in airports, planes, stations, and trains. My physical conference trips used to provide ample idle time. I used that time to contact colleagues to schedule a dinner, lunch, or coffee at the conference; to read the conference program and highlight the talks I wanted to see; to check out the map of the venue to know where to find the relevant rooms; and even to read a paper or two to prepare for talking to the authors at the conference.

That kind of preparation takes more than a second. And without the time provided by those arduous trips, I might show up ill prepared and miss out on half of the fun.

So here is my plan. For my next one-second conference trip, I will allocate a little bit of extra time to prepare. Not crammed into an airplane seat, but at home, in a comfy chair, with a nice cup of coffee.

Oh, and if your next conference trip takes you to ICER 2021 this coming Monday, here are some suggestions from the ICER Chairs for how to prepare for this conference, which will be hosted in the most recent version of Clowdr:

• Find the invitation email you received from Clowdr (check your spam folder, too!) and log in (3 minutes).
• Watch the ICER 2021 Clowdr Intro video (13 minutes). This will teach you the basics of how to navigate the platform. We recommend following along interactively on the Clowdr site as you watch, to familiarize yourself with the navigation
• Watch the ICER 2021 Paper Sessions: Participant Experience video (14 minutes). This will teach you how our paper sessions will work. You won’t just be watching videos, you’ll also be interacting while you watch, talking in small groups afterwards, and asking questions.
• Once logged in, read the ICER Clowdr Experience FAQ page (4 minutes). This has the videos above and more detail for specific types of events.
• On Clowdr, read the Code of Conduct page (3 minutes). Everyone is responsible for following these rules to ensure everyone feels safe and welcome.
• On Clowdr, read the How to Set Up Your Profile page and set up your profile (3 minutes). This ensures people know who you are, what your name and pronouns are, where you’re visiting from, and what roles you’re playing at the conference. 

In Clowdr you will find a lot of content, including the entire program. We recommend that inside Clowdr you “star” events you are interested in to create your personal schedule. There is a page for each paper and poster/lightning talk. On each paper page you already find the presentation as an embedded video, on each ICER poster page there’s the poster pitch video and the PDF of the poster, and on each ICER lightning talk page you find the talk slide. Have a quick look to plan your personal schedule. And while you’re there, why not already leave a message or comment for the authors in the chat at the right of the paper/poster’s page? Note that the links to the papers in the ACM DL are not yet active; we expect ACM to make the DOIs work and the papers visible in the DL by the start of the conference.

We are confident that with an hour or so of up-front effort you will get much more out of the conference! (We suspect, though, that you will end up spending more than an hour because the content draws you in!) ICER 2021 is a compact conference packed with exciting content and interaction. Log in now to make the most of it!

*) I also very much love the minimal carbon footprint, low cost, and reduced health risks of virtual conferences.

Why aren’t more girls in the UK choosing to study computing and technology? Guest blog post by Peter Kemp

The Guardian raised the question in the title in this article in June. Pat Yongpradit sent it to me and Peter Kemp, and Peter’s response was terrific — insightful and informed by data. I asked him if I could share it here as a guest post, and he graciously agreed.

We’ve just started a 3 year project, scaricomp, that aims to look at girls’ performance and participation in computer science in English schools. There’s not much to see at the moment, as we started in April, but we’re hoping to sample 5000+ students across schools with large numbers of students taking CS and/or high numbers of females in the CS cohorts. I’ll let you know when we have some analysis in hand.

You reference The Guardian article’s quote: “In 2019, 17,158 girls studied computer science, compared with the 20,577 girls who studied ICT in 2018”. It’s worth noting that the 2018 ICT figure was the end of the line for ICT, numbers in previous years were much higher, and the female figure was actually ~40% of the overall ICT entries, whilst it represents about 20% of the GCSE CS cohort, i.e. females were proportionally better represented in ICT than CS. For a fuller picture of the changing numbers and demographics in English computing, see slide 8 of this, or the video presentation). It’s also worth noting that since the curriculum change in 2012/13 we’ve lost the majority of time dedicated to teaching computing (including CS) at age 14-16, I’ve argued that this has had a disproportionate impact on girls and poorer students (page 45-48).

To add a bit of context from England: Students typically pick 8-10 subjects for GCSE, though their ‘options’ might be limited. Most schools will insist that students take Maths, English Language, English Literature, Physics, Chemistry, Biology, and often: French or German, and History or Geography. This leaves students with one or two actual ‘options’. Many schools are also imposing entry requirements on GCSE CS, only letting the high achieving students (often focusing on maths) onto the course; this will likely have an impact in access to the curriculum for poorer students who are less likely to achieve well in mathematics. Why don’t females pick CS in the same way they picked ICT? This might well be linked to curriculum, role models, contextualisation etc.

One of the reasons given for the curriculum change in 2012 was that students were being “bored to death” by ICT, with ICT generally being the application of software products to solve problems and the implication of technology on the world. The application of technology to the world lends itself to the contextualisation of the curriculum and the assessment materials. There was a lot of project-based assessment with real world scenarios for students to engage with, e.g. making marketing materials for businesses, using spreadsheets to organise holiday bookings etc https://web.archive.org/web/20161130183550if_/http://www.aqa.org.uk/subjects/computer-science-and-it/gcse/information-and-communication-technology-4520) . The GCSE CS is a different beast. It can be contextualised, but this is probably more difficult to do as there is an awful lot of material to cover and the assessment methodology is entirely exam based and on paper for the largest exam boards. Anecdotally we hear of schools cutting down on programming time on computers, as the exam is handwritten.

Data looking at what females ‘liked’ in the old ICT curriculum is quite limited, but what does exist places some of the ‘non-CS’ elements quite highly. So, the actual curriculum content might have a part to play here. Having taught ICT (and CS) for many years, most students I knew really enjoyed the ICT components. I’d argue that the pre-reform discourse around ICT being: “useless, boring, easy”, CS being: “useful, exciting, rigorous” was an easy political position to take, and not reflective of reality where schools had competent teachers. We now find ourselves in a position where we probably have a little too much CS, and not enough digital literacy / ICT for the general needs of students. I and people like Miles Berry (p49) have argued for more generalist qualification which maintains elements of CS. Though there appears to be little political will to make this happen.

To add another suggestions as to why we’re seeing females disengaging, within the English context, we see females substantially underachieving at GCSE in comparison to their other subjects and males of similar ‘abilities’ (ability here being similar grade profiles in other subjects). Why this is remains unclear, we see similar under achievement in Maths and Physics. My fear is that encouraging females to take CS might lead them to having their self-efficacy knocked and therefore make them less likely to pursue further study or a career in tech. We also found that females from poorer backgrounds were more likely to pick GCSE CS than their middle-class peers, we speculate that this might be the result of different cultural/family pressures and a keener engagement with the ’employability’ and ‘good pay’ discourse that often surrounds the representation of studying CS, however true this might be for these groups in reality. More research on the above coming soon through scaricomp.

Additionally, in terms of the UK picture, you’ll probably want to check in with Sue Sentance and the Gender Balance in Computing Project. One of their theories for the decline in computing is that CS is being timetabled at the same time as other (generally) more attractive subjects for females. I’m not sure if they’ve started this part of the research yet, but it’s worth checking in. They are running interventions across the country, but I don’t believe that they are trying to do a nationally representative survey.

There is transfer between programming and other subjects: Skills overlap, but it may not be causal

A 2018 paper by Ronny Scherer et al. “The cognitive benefits of learning computer programming: A meta-analysis of transfer effects” was making the rounds on Twitter. They looked at 105 studies and found that there was a measurable amount of transfer between programming and situations requiring mathematical skills and spatial reasoning. But here’s the critical bit — it may not be casual. We cannot predict that students learning programming will automatically get higher mathematics grades, for example. They make a distinction between near transfer (doing things that are very close to programming, like mathematics) and far transfer, which might include creative thinking or metacognition (e.g., planning):

Despite the increasing attention computer programming has received recently (Grover & Pea, 2013), programming skills do not transfer equally to different skills—a finding that Sala and Gobet (2017a) supported in other domains. The findings of our meta-analysis may support a similar reasoning: the more distinct the situations students are invited to transfer their skills to are from computer programming the more challenging the far transfer is. However, we notice that this evidence cannot be interpreted causally—alternative explanations for the existence of far transfer exist.

Here’s how I interpret their findings. Learning program involves learning a whole set of skills, some of which overlap with skills in other disciplines. Like, being able to evaluate an expression with variables, once you know the numeric value for those variables — you have to do that in programming and in mathematics. Those things transfer. Farther transfer depends on how much overlap there is. Certainly, you have to plan in programming, but not all of the sub-skills for the kinds of planning used in programming appear in every problem where you have to plan. The closer the problem is to programming, the more that there’s an overlap, and the more we see transfer.

This finding is like a recent paper out of Harvard (see link here) that shows that AP Calculus and AP CS both predict success in undergraduate computer science classes. Surprisingly, regular (not AP) calculus is also predictive of undergraduate CS success, but not regular CS. There are sub-skills in common between mathematics and programming, but the directionality is complicated.

We have known for a long time that we can teach programming in order to get a learning effect in other disciplines. That’s the heart of what Bootstrap does. Sharon Carver showed that many years ago. But that’s different than saying “Let’s teach programming, and see if there’s any effect in other classes.”

So yes, there is transfer between programming and other disciplines — not that it buys you much, and the effect is small. But we can no longer say that there is no transfer.

Rules work as a way of communicating computation at a mechanistic level without teaching programming

Sometimes as a reviewer, you get to read a paper that you wish was published immediately. That’s how I felt when I got to review Eliane Wiese and Marcia Linn’s paper “It Must Include Rules”: Middle School Students’ Computational Thinking with Computer Models in Science. It was published in ACM TOCHI in April (see link here).

Eliane and Marcia offer a solution to a problem that teachers face when they want to teach about computational models, but they don’t want to teach programming. How do you get students to reason about the models underlying the simulations they’re exploring without talking about program code? And if you do talk about some notation, some representation of the model, what can you expect students to reason about without teaching them the notation or representation first?

Eliane and Marcia show that rules work. They have students interact with simulations, and then show them rules that might be in that model. Like in a simulation of light, photosynthesis, and glucose levels in plants, a rule might be: When light is on, total glucose made increases.. Eliane and Marcia show rules to students and ask “Are these in the model?” In their abstract, they write:

In our sample, 99% of students identified at least one key rule underlying a model, but only 14% identified all key rules; 65% believed that model rules can contradict; and 98% could not distinguish between emergent patterns and behaviors that directly resulted from model rules. Despite these misconceptions, compared to the “typical” questions about the science content alone, questions about model rules elicited deeper science thinking, with 2–10 times more responses including reasoning about scientific mechanisms. These results suggest that incorporating computational thinking instruction into middle school science courses might yield deeper learning and more precise assessments around scientific models.

The misconceptions don’t bother me. Students will have misconceptions about models — that’s part of teaching science with models. What’s fascinating to me is that the rules worked. Students reasoned mechanistically about the computational models.

My favorite result in this study was where they asked students to predict what would happen if they added a new rule to the model. Basically, “What happens if we change the program like this?” Students were way better at playing these what-if games if the question was posed as a rule. Quoting from the paper:

Asking students to make predictions about the implementation of incorrect rules led to more scientific reasoning about mechanisms than simply asking students about a causal relationship portrayed in a correct model. This pattern was evident for both model contexts, with twice as many workgroups proposing mechanisms with the New Rule question compared to the Typical question for Global Climate (29% vs. 14%) and ten times as many workgroups doing so for Chemical Reactions (53% vs. 5%).

Students can reason about computational models described as rules, even without instruction on rules. That’s a terrific result. It’s one that I’m thinking about how to use in my task-specific programming languages.

Now, this isn’t saying that students can’t reason with function or with imperative statements. Maybe functional or procedural programming paradigms would work, too. Eliane and Marcia have found one approach that does work. They offer us a way to integrate computational modeling into science education, with real discussion of the mechanism of the models, without teaching programming first.