Thought Experiments on Why Face-to-Face Teaching Beats On-Line Teaching: We are Humans, not Econs

With everything moving on-line, I’m seeing more discussion about whether this on-line life might just be better. Amy Ko recently blogged (see post here) about how virtual conferences are cheaper, more accessible, and lower carbon footprint than face-to-face conferences, ending with the conclusion for her “it is hard to make the case to continue meeting in person.” My colleague, Sarita Yardi, has been tweeting about her exploration of “medium-independent classes” where she considers (see tweet here), “Trying to use the block of class time just because that’s how we’ve always taught seems like something to revisit. Less synchronous time; support short, frequent individual/small group interaction, less class time.”

It’s hard to do on-line education well. I used to study this kind of learning a lot (see post on “What I have learned about on-line collaborative learning”). I recently wrote about how we’re mostly doing emergency remote teaching, not effective on-line learning (see post here). I am concerned that moving our classes on-line will hurt the most the students who most need our help (see post here).

It should come as no surprise then that I don’t think that we know how to do on-line teaching or on-line conferences in a way that is anywhere close to the effectiveness of face-to-face learning. I agree with both Amy and Sarita’s points. I’m only focusing on learning outcomes.

Let me offer a thought experiment on why face-to-face matters. How often do you…

• Look at the movie trailer and not watch the movie.
• Watch the first few minutes of a show on Netflix but never finish it.
• Start a book and give up on it.
• Start watching a YouTube video and immediately close it or click away.

Now contrast that with: How often do you…

• Get up from a one-on-one meeting and walk out mid-discussion.
• Get up in the middle of a small group discussion and leave.
• Walk out of a class during a lecture.
• Walk out of a conference session while the speaker is still presenting (not between talks or during Q&A).

For some people, the answers to the first set are like the answers for the second set. I tried this thought experiment on my family, and my wife pointed out that she finishes every book she starts. But for most people, the first set is much more likely to happen than the second set. This is particularly hard for professors and teachers to recognize. We are good at self-regulated learning. We liked school. We don’t understand as well the people who aren’t like us.

There are a lot of people who don’t really like school. There are good reasons for members of minority groups to distrust or dislike school. Most people engage in higher-education for the economic benefit. That means that they have a huge value for the reward at the end, but they don’t particularly want to go through the process. We have to incentivize them to be part of the process.

Yes, of course, many students skip classes. Some students skip many classes. But the odds are still in favor of the face-to-face classes. If you are signed up for a face-to-face class, you are much more likely to show up for that class compared to any totally free and absolutely relevant to your interests lecture, on-campus or on-line. Enrolling in a course is a nudge.

For most people, you are much more willing to walk away from an asynchronous, impersonal event than a face-to-face, personal event. The odds of you learning from face-to-face learning are much higher simply because you are more likely to show up and less likely to walk out. It’s a great design challenge to make on-line learning opportunities just as compelling and “sticky” as face-to-face learning. We’re not there yet.

I would be all in favor of efforts to teach people to be more self-regulated. It would be great if we all were better at learning from books, lectures, and on-line resources. But we’re not. The learners with the best preparation are likely the most privileged students. They were the ones who were taught how to learn well, how to learn from school, and how to enjoy school.

Here’s a second thought experiment, for people who work at Universities. At any University, there are many interesting talks happening every week. For me, at least a couple of those talks each week are faculty candidates, which I am highly encouraged to attend. Now, they’re all on-line. How many of those did you attend when they were face-to-face, and how many do you attend on-line? My guess is that both are small numbers, but I’ll bet that the face-to-face number is at least double the on-line number. Other people see that you’re there face-to-face. There are snacks and people to visit with face-to-face. The incentives are far fewer on-line.

On-line learning is unlikely to ever be as effective as face-to-face learning. Yes, we can design great on-line learning, but we do that fighting against how most humans learn most things. Studies that show on-line learning to be as effective (or even more effective) than face-to-face classes are holding all other variables equal. But holding all other variables equal takes real effort! To get people to show up just as much, to give people as much (or more) feedback, and to make sure that the demographics of the class stay the same on-line or face-to-face — that takes significant effort which is invisible in the studies that are trying to just ask face-to-face vs on-line. The reality is that education is an economic endeavor. Yes, you can get similar learning outcomes, at a pretty high cost. At exactly the same cost, you’re unlikely to get the same learning outcomes.

We are wired to show-up and learn from face-to-face events. I would love for all of us to be better self-regulated learners, to be better at learning from books and from lecture. But we’re not Econs, we’re Humans (to use the Richard Thaler distinction). We need incentives. We need prompts to reflect, like peer instruction. We need to see and be seen, and not just through a small box on a 2-D screen.

What do I mean by Computing Education Research? The Computer Science Perspective

 

Last week, I talked about how I explain what I do to social scientists. This time, let me explain what I do to computer scientists. I haven’t given this talk yet, and have only tried the ideas out on a few people. So consider this an experiment, and I’d appreciate your feedback.

Let’s simplify the problem of computing education research (maybe a case of a spherical cow). Let’s imagine that instead of classes of Real Humans, we are teaching programming to Human-like Turing Machines (HTMs). I’m not arguing that Turing machines are sufficient to represent human beings. I’m asking you to believe that (a) we might be able to create Turing Machines that could simulate humans, like those we have in our classes, (b) RH’s would only have additional capabilities beyond what HTM’s have, and (c) HTM’s and RH’s would similar mechanisms for cognition and learning. (Carl Hewitt has a great CACM blog post arguing that message passing is more powerful than TM’s or first order logic, so maybe these should be HMP, Human Message Passers. I don’t think I need more than TM’s for this post.)

This isn’t a radical simplification. Cognitive science started out using computation as a model for understanding cognition (see history here). Information processing theory in psychology starts from a belief that humans process information like a computer (see Wikipedia article and Ed Psychology reference). Newell and Simon won the ACM Turing award and in their Turing Award lecture introduced the physical symbol system hypothesis, “A physical symbol system has the necessary and sufficient means for general intelligent action.” If we have a program on a Turing machine that gives it the ability to process the world in symbols, our theory suggests that it would be capable of intelligence, even human-like intelligence. I’m applying this lens to how we think about humans learning to program.

This simplification buys me two claims:

• The Geek Gene is off the table. The Geek Gene is the belief that some people can’t learn to program (see blog post for more). Any Turing machine can simulate any other Turing machine. Our HTM’s are capable of tracing a program. If any HTM can also write code, then all HTM’s can write code. Everyone has the same computational capability. (If HTM’s can all code, then RH’s can all code, because HTM’s have a subset of RH cognitive capabilities.)
• Learning of our students can be analyzed and understood as information processing. The behavior of Turing machines is understandable with analysis. HTM’s are sophisticated Turing machines. The core mechanism of HTM’s can be analyzed and understood. If we think about our students as HTM’s, we might reason about their learning about computing.

Here are some of the research questions that I find interesting, within this framing.

How do HTM’s learn to program?

All HTM’s must learn, and learn at a level where their initial programming (the bootstrap code written on their tape when they come into our world) becomes indistinguishable from learned capabilities. HTM’s must have built-in programming to eat and to sleep. They learn to walk and run and decipher symbols like “A,” such that it’s hard to tell what was pre-programmed and what was learned. HTM’s can extend their programming.

There are lots of models that describe how HTM’s could learn, such as SOAR and ACT-R. But none so far has learned to program. The closest are the models used to build the cognitive tutors for programming, but those couldn’t debug and couldn’t design programs. They could work from a definition of a program to assemble a program, but that’s not what most of us would call coding. How would they do it?

How would HTM’s think about code? How would it be represented in memory (whether that memory is a tape, RAM, or human brains)? There is growing research interest in how people construct mental models of notional machines. Even experts don’t really know the formal semantics of a language. So instead, they have a common, “notional” way of thinking about the language. How does that notional machine get represented, and how does it get developed?

How do we teach HTM’s to learn to program?

You shouldn’t be able to just reprogram HTM’s or extend their programs by some manipulation of the HTM’s. That would be dangerous. The HTM might be damaged, or learn something that led them into danger. Instead, extending HTM’s programming can only be done by conscious effort by the HTM. That’s a core principle of Piaget’s Theory of Cognitive Development — children (RH’s and HTM’s) learn by consciously constructing a model of the world.

So, we can’t just tell an HTM how to program. Instead, we have to give them experiences and situations where they learn to program when trying to make sense of their world. We could just make them program a lot, on increasingly harder programs. Not only is that de-motivating (maybe not an issue for HTM’s, but certainly is for RH’s), but it’s inefficient. Turns out that we can use worked examples with subgoal labeling and techniques like Parson’s problems and peer instruction to dramatically improve learning in less time.

What native capabilities of HTM’s are used when they learn to code?

We know that learning to read involves re-using more primitive mechanisms to see patterns (see article here). When HTM’s learn to program, what parts of the native programming are being re-used for programming?

Programming in RH’s may involve re-use of our built-in ability to reason about space and language. My colleague Wes Weimer (website) is doing FMRI studies showing that programmers tend to use the parts of their brain associated with language and spatial reasoning. In our work, we have been studying the role of spatial reasoning and gesture in learning to program (see summaries of our ICER 2018 papers). We don’t know why spatial reasoning might be playing a role in learning to program. Maybe it’s not spatial reasoning, but some aspect of spatial reasoning or maybe it’s even some other native ability that is related to spatial reasoning.

How does code work as an external representation of HTM’s, and where does it help?

We can safely assume that HTM’s, like RH’s, would enhance their cognition through the use of external representations. Cognition and memory are limited. Even an infinite tape has limitations in terms of time to access. Human cognitive systems are limited in terms of how much can be attended to at once. RH’s use external representations (writing notes, making diagrams, sketches) to enhance their cognition. We’re assuming that HTM’s have a subset of RH abilities, so external representations would help HTM’s, too.

My students and I talk about a wonderful paper by David Kirsh, Thinking with External Representations (see link here). It’s a compelling view of how external representations give us abilities to think that we don’t have with just our brain alone.

How can program code be a useful external representation for HTM’s? When does it help, e.g., with what cognitive tasks is code a useful external representation? For example, a natural one is modeling and simulation — we can model more complex situations with program code than we can keep in our head, and we can simulate that model for a much larger range of time and possible values. Are there cognitive tasks where code by itself, as a notation like written language or mathematics, can enhance cognition? Here I’m thinking about the ability of code to represent causal relationships (e.g., as in Bruce Sherin’s work) or algebraic forms (e.g., as in Bootstrap) — see here for discussion of both.  I’m intrigued by the idea of the affordances of reading code even before writing it.

What makes programming worth learning for HTM’s?

Why should an HTM learn programming? Let’s assume that an HTM’s basic programming is going to be about staying alive, e.g., Maslow’s hierarchy of needs. When would an HTM want to learn programming?

The most obvious reason to learn programming is because you can get paid to do it. It’s about meeting physiological needs and safety. But, if you can meet those needs doing something that’s easier or more pleasant or has fewer barriers, you’ll likely do that.

Sometimes, you’ll want to learn programming because it makes easier something you want to do anyway. Brian Dorn’s graphic designers wanted to learn programming (see here) because they used Photoshop or GIMP and wanted a way to do that easier and faster. Maybe that’s about safety and physiological needs, but maybe it was about esteem or even self-actualization (if HTM’s care about those things).

Where my simplification breaks down: Real humans learn in situated and social contexts

Our learning theory about RH’s say that they are unlikely to start a new subject unless there’s social pressure to do so (see Pat Alexander’s Model of Domain Learning). Would HTM’s feel social pressure? Maybe.

As I described in the previous blog post, much of my work is framed around sociocultural models of learning, like Lave and Wenger’s situated learning. I use Communities of Practice to understand a lot of the situations that I explore. We can only go so far in thinking about programming as just being inside of individual minds (HTM or RH). Much of the interesting stuff comes when we realize that (a) our cognition interacts with the environments and situations around us, and (b) our motivation, affect, and cognition are influenced by our social world.

Setting aside whether it’s social science or computer science, I am still driven by a paper I read in 1982, which was five years after it was written: “Personal Dynamic Media” by Alan Kay and Adele Goldberg (see copy here).  I want people to be to use coding like they use other literacies, to create a literature, and in a casual, informal and still insightful way.  Mitchel Resnick often talks about people using Scratch to write a card to their mother or grandmother — that’s the kind of thing I want to see.  I want people to be able to make small computational models that answer questions, in the same way that people do “back of the envelope” calculations today. I also want great literature — we need Shakespeares and daVinci’s who convey great thoughts with computing (an argument that Andrea diSessa made recently at the PPIG conference which Felienne Hermans blogged about here.) That’s the vision that drives me, whether I’m using cognitive science or situated learning.

 

Applying diSessa’s Knowledge in Pieces Framework to Understanding the Notional Machine

In Lauren Margulieux’s blog where she summarizes papers from learning sciences and educational psychology, she takes on Andy diSessa’s 1993 paper “Toward an epistemology of physics” where diSessa applies his “knowledge in pieces” framework to how students develop an understanding of physics.  (See blog post here.)

The idea is that humans assemble their understanding of complex phenomenon out of knowledge of physical experiences, p-prims. Quoting Lauren:

Elements: P-prims are knowledge structures that are minimal abstractions of common phenomena and typically involve only a few simple parts, e.g., an observed phenomenon, like a person hitting a pen and that pen rolling across the table, and an explanation, like when people hit things, they move. P-prims are both phenomenological, meaning that they are interpretations of reality, and primitive, meaning that are (1) based on often rudimentary self-explanations and (2) an atomic-level mental structure that is only separated into parts by excessive force.

Cognitive Mechanism: P-prims are only activated when the learner recognizes similarities between a p-prim and the current phenomena. Recognition is impacted by many different features, such as cuing, frequency of activation, suppression, salience, and reinforcement. Because activation of p-prims depends on contextual features of phenomena, novices often fail to recognize relevant p-prims unless the contextual features align.

I find diSessa’s framework fascinating, and I’ve always wondered how we could apply it to students learning the notional machine (see blog post here on notional machine). My guess is that students use p-prims to develop their mental model of how the computer works, because — what else could they use? In the end, isn’t all our understanding grounded in physical experiences?  But using p-prims will likely lead to misconceptions since the notional machine is not based in the physical world.

Maybe this is a source of common misconceptions in learning computing.  The list of misconceptions that students have about variables, loops, scope, conditionals, and data structures is long and surprisingly consistent — across languages, over time.  What could possibly be the common source of all those misconceptions?  Maybe it’s physical reality.  Maybe students generally apply the same p-prims when trying to understand computing, and that’s why the same misconceptions arise. It’s sort of like using a metaphor to understand something in computing, but then realizing that the metaphor itself is leading to misconceptions.  And the metaphor that’s getting in our way is the use of physical world primitives for understanding the computational world.

Colleen Lewis, as a student of diSessa’s, uses the Knowledge in Pieces framework in her work.  In her terrific ICER 2012 paper, she does a detailed analysis of students’ debugging to identify misconceptions that they have about state. State is an interesting concept to study from a KiP perspective. It’s a common issue in CS, but less common in Physics. It’s not clear to me how students connect computational state to state in the real world.  Is it state like water being frozen or liquid, or state like being painted blue?  Do they get that state is malleable?

This is a rich space to explore in computing education. What are the p-prims for understanding the notional machine? How do students use the physical world to understand the computational one?

Read more of Lauren’s post here: Article Summary: diSessa (1993) Knowledge in Pieces Framework

How computing education researchers and learning scientists might better collaborate

Lauren Margulieux has started a blog which is pretty terrific.  I wrote about Lauren’s doctoral studies here, and I last blogged about her work (a paper comparing learning in programming, statistics, and chemistry) here.

In her blog, Lauren is explaining in lay terms papers from learning sciences, educational psychology, and educational technology.  She’s an interdisciplinary researcher, and she’s blogging to help others connect across disciplines.

Her most recent blog post is about an issue I’ve been thinking about a lot lately. I wrote a blog post in the summer about the challenge of bridging the modes of science and truth-seeking in (computing) education vs. computer science. Lauren summarizes a paper by Peffer and Renken about concrete strategies to be used between discipline-based education researchers (like math education researchers, science education researchers, or computing education researchers) and learning scientists. Quoting part of it below:

Challenges in Interdisciplinary Research: Collaboration within a field can be difficult as people attempt to reconcile different ideas towards one goal. Collaboration between fields, each with its own traditions in theory and methodology, can seem like a minefield. Below are some common challenges that DBERers and learning scientists face.

1. Differences in hard and soft sciences – researchers in the hard sciences can often feel frustrated by the lack of predictability in human-subjects research, and researchers in social sciences can become frustrated when those in the hard sciences have unrealistic expectations or view research in the soft sciences as non-scientific.

2. Differences in theories and frameworks – What constitutes a theory or framework can be different in different domains, confusing what is often a fundamental building block of research.

3. Differences in research methodologies – those unfamiliar with human-subjects research can find its methodologies complex, varied, and full of uncertainty, and those who have endured countless hours of training in these methodologies can find it difficult to describe or justify methodological decisions in a concise way.

See more at https://laurenmarg.com/2018/07/29/peffer-renken-2016-dber-and-learning-sciences-collaboration-strategies/

Learning Myths And Realities From Brain Science

Interesting results, but also, concerning.  People really believe that intelligence is “fixed at birth” and that teachers don’t need to know content?  The article has more of these:

On the topic of “growth mindset,” more than one-quarter of respondents believed intelligence is “fixed at birth”. Neuroscience says otherwise.

Nearly 60 percent argued that quizzes are not an effective way to gain new skills and knowledge. In fact, quizzing yourself on something you’ve just read is a great example of active learning, the best way to learn.

More than 40 percent of respondents believed that teachers don’t need to know a subject area such as math or science, as long as they have good instructional skills. In fact, research shows that deep subject matter expertise is a key element in helping teachers excel.

Source: Learning Myths And Realities From Brain Science : NPR Ed : NPR

Power law of practice in software implementation: Does this explain the “W” going away?

I wonder if this result explains why the second semester students in Briana’s studies (see previous blog post) didn’t have the “W” effect.  If you do enough code, you move down the power law of practice, and now you can attend to things like context and generating subgoal labels.

Different subjects start the experiment with different amounts of ability and past experience. Before starting, subjects took a multiple choice test of their knowledge. If we take the results of this test as a proxy for the ability/knowledge at the start of the experiment, then the power law equation becomes (a similar modification can be made to the exponential equation):

That is, the test score is treated as equivalent to performing some number of rounds of implementation). A power law is a better fit than exponential to this data (code+data); the fit captures the general shape, but misses lots of what look like important details.

Source: The Shape of Code » Power law of practice in software implementation

Graduating Dr. Briana Morrison: Posing New Puzzles for Computing Education Research

I am posting this on the day that I am honored to “hood” Dr. Briana Morrison. “Hooding” is where doctoral candidates are given their academic regalia indicating their doctorate degree. It’s one of those ancient parts of academia that I find really cool. I like the way that the Wikiversity describes it: “The Hooding Ceremony is symbolic of passing the guard from one generation of doctors to the next generation of doctors.”

I’ve written about Briana’s work a lot over the years here:

• Her proposal is described here, “Cognitive Load as a significant problem in Learning Programming.”
• Her first major dissertation accomplishment was developing (with Dr. Brian Dorn) a measurement instrument for cognitive load.
• One of her bigger wins for her dissertation was showing that subgoal labels work for text languages too (ICER 2015).
• Another really significant result was showing that Parson’s Problems were a more sensitive measure of learning than asking students to write code in an assessment, and that subgoal labels make Parson’s Problems better, too.
• She worked a lot with Lauren Margulieux, so many of the links I listed when Dr. Margulieux defended are also relevant for Dr. Morrison.
• At ICER 2016, she presented a replication study of her first given vs. generated subgoals study.

But what I find most interesting about Briana’s dissertation work were the things that didn’t work:

• She tried to show a difference in getting program instruction via audio or text. She didn’t find one. The research on modality effects suggested that she would.
• She tried to show a difference between loop-and-a-half and exit-in-the-middle WHILE loops. Previous studies had found one. She did not.

These kinds of results are so cool to me, because they point out what we don’t know about computing education yet. The prior results and theory were really clear. The study was well-designed and vetted by her committee. The results were contrary to what we expected. WHAT HAPPENED?!? It’s for the next group of researchers to try to figure out.

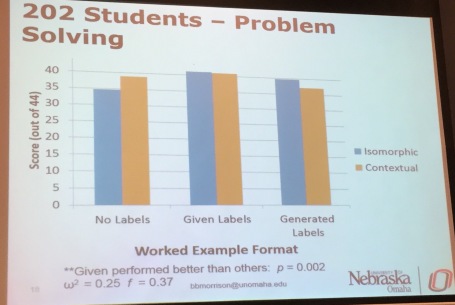
The most interesting result of that kind in Briana’s dissertation is one that I’ve written about before, but I’d like to pull it all together here because I think that there are some interesting implications of it. To me, this is a Rainfall Problem kind of question.

Here’s the experimental set-up. We’ve got six groups.

1. All groups are learning with pairs of a worked example (a completely worked out piece of code) and then a practice problem (maybe a Parson’s Problem, maybe writing some code). We’ll call these WE-P pairs (Worked Example-Practice). Now, some WE-P pairs have the same context (think of it as the story of a story problem), and some have different contexts. Maybe in the same context, you’re asked to compute the average tips for several days of tips as a barista. Maybe in a different context, you compute tips in the worked example, but you compute the average test score in the practice. In general, we predict that different contexts will be harder for the student than having everything the same.
2. So we’ve got same context vs different context as one variable we’re manipulating. The other variable is whether the participants get the worked example with NO subgoal labels, or GENERATED subgoal labels, or the participant has to GENERATE subgoal labels. Think of a subgoal label as a comment that explains some code, but it’s the same comment that will appear in several different programs. It’s meant to encourage the student to abstract the meaning of the code.

In the GENERATE condition, the participants get blanks, to encourage them to abstract for themselves. Typically, we’d expect (for research in other parts of STEM with subgoal labels) that GENERATE would lead to more learning than GIVEN labels, but it’s harder. We might get cognitive overload.

In general, GIVEN labels beats out no labels. No problem — that’s what we expect given all the past work on subgoal labels. But when we consider all six groups, we get this picture.

Why would having the same context do worse with GIVEN labels than no labels? Why would the same context do much better with GENERATE labels, but worse when it’s different contexts?

So, Briana, Lauren, and Adrienne Decker replicated the experiment with Adrienne’s students at RIT (ICER 2016). And they found:

The same strange “W” pattern, where we have this odd interaction between context and GIVEN vs. GENERATE that we just don’t have an explanation for.

But here’s the really intriguing part: they also did the experiment with second semester students at RIT. All the weird interactions disappeared! Same context beat different context. GIVEN labels beat GENERATE labels. No labels do the worst. When students get enough experience, they figure things out and behave like students in other parts of STEM.

The puzzle for the community is WHY. Briana has a hypothesis. Novice students don’t attend to the details that they need, unless you change the contexts. Without changing contexts, students even GIVEN labels don’t learn because they’re not paying enough attention. Changing contexts gets them to think, “What’s going on here?” GENERATE is just too hard for novices — the cognitive load of figuring out the code and generating labels is just overwhelming for students, so they do badly when we’d expect them to do better.

Here we have a theory-conflicting result, that has been replicated in two different populations. It’s like the Rainfall Problem. Nobody expected the Rainfall Problem to be hard, but it was. More and more people tried it with their students, and still, it was hard. It took Kathi Fisler to figure out how to teach CS so that most students could succeed at the Rainfall Problem. What could we teach novice CS students so that they avoid the “W” pattern? Is it just time? Will all second semester students avoid the “W”?

Dr. Morrison gave us a really interesting dissertation — some big wins, and some intriguing puzzles for the next researchers to wrestle with. Briana has now joined the computing education research group at U. Nebraska – Omaha, where I expect to see more great results.

How to Write a Guzdial Chart: Defining a Proposal in One Table

In my School, we use a technique for representing an entire research proposal in a single table. I started asking students to build these logic models when I got to Georgia Tech in the 1990’s. In Georgia Tech’s Human-Centered Computing PhD program, they have become pretty common. People talk about building “Guzdial Charts.” I thought that was cute — a local cultural practice that got my name on it.

Then someone pointed out to me that our HCC graduates have been carrying the practice with them. Amy Voida (now at U. Colorado-Boulder) has been requiring them in her research classes (see syllabus here and here). Sarita Yardi (U. Michigan) has written up a guide for her students on how to summarize a proposal in a single table. Guzdial Charts are a kind of “thing” now, at least in some human-centered computing schools.

Here, I explain what a Guzdial Chart is, where it came from, and why it should really be a Blumenfeld Chart [*].

Phyllis Teaches Elliot Logic Models

In 1990, I was in Elliot Soloway’s office at the University of Michigan as he was trying to explain an NSF proposal he was planning with School of Education professor, Phyllis Blumenfeld. (When I mention Phyllis’s name to CS folks, they usually ask “who?” When I mention her name to Education folks, they almost always know her — maybe for her work in defining project-based learning or maybe her work in instructional planning or maybe her work in engagement. She’s retired now, but is still a Big Name in Education.) Phyllis kept asking questions. “How many students in that study?” and “How are you going to measure that?” She finally got exasperated.

She went to the whiteboard and said, “Draw me a table like this.” Each row of the table is one study in the overall project.

• Leftmost column: What are you trying to achieve? What’s the research question?
• Next column: What data are you going to collect? What measures are you going to use (e.g., survey, log file, GPS location)?
• Next column: How much data are you going to collect? How many participants? How often are you going to use these measures with these participants (e.g., pre/post? Midterm? After a week delay?)?
• Next column: How are you going to analyze these data?
• Rightmost column: What do you expect to find? What’s your hypothesis for what’s going to happen?

This is a kind of a logic model, and you can find guides on how to build logic models. Logic models are used by program evaluators to describe how resources and activities will lead to desired impacts. This is a variation that Phyllis made us use in all of our proposals at UMich. (Maybe she invented it?) This version focused on the research being proposed. Each study reads on a row from left-to-right,

• from why you were doing it,
• to what you were doing,
• to what you expected to find.

When I got to Georgia Tech, I made one for every proposal I wrote. I made my students do them for their proposals, too. Somewhere along the way, lots of people started doing them. I think Beth Mynatt first called them “Guzdial Charts,” and despite my story about Phyllis Blumenfeld’s invention, the name stuck. People at Georgia Tech don’t know Phyllis, but they did know Guzdial.

Variations on a Guzdial Chart Theme

The critical part of a Guzdial Chart is that each study is one row, and includes purpose, methods, and expected outcome. There are lots of variations. Here’s an example of one that Jason Freeman (in our School of Music) wrote up for a proposal he was doing on EarSketch. He doesn’t list hypotheses, but it still describes purpose and methods, one row per study.

In Sarita’s variation, she has the students put the Expected Publication in the rightmost column. I like that — very concrete. If you’re in a discipline with some clearly defined publication targets, with a clear distinction between them (e.g. , the HCI community where Designing Interactive Systems (DIS) is often about process, and User Interface Software and Technology (UIST) is about UI technologies), then the publication targets are concrete and definable.

My former student, Mike Hewner, did one of the most qualitative dissertations of any of my students. He used a Guzdial Chart, but modified it for his study. Still one row per study, still including research question, hypothesis, analysis, and sampling.

I still use Guzdial Charts, and so do my students. For example, we used one to work through the story for a paper. Here’s one that we started on a whiteboard outside of my office, and we left it there for several weeks, filling in the cells as they made sense to us.

A Guzdial Chart is a handy way of summarizing a research project and making sure that it makes sense (or to use when making sense), row-by-row, left-to-right.

 

___________

[*] Because Ulysses now makes it super-easy to post to blogs, and I do most of my writing in Ulysses, I accidentally posted this post to Medium — my first ever Medium post.  I wanted this to appear in my WordPress blog, also, so I decided to two blog posts: The Medium one on Blumenfeld Charts, and this one on Guzdial Charts.

Making learning effective, efficient, and engaging: An Interview With an Educational Realist and Grumpy Old Man, Paul Kirschner

I am a fan of Paul Kirschner‘s work.  This interview is great with useful insights about education — deep and pragmatic thinking.

I want to fundamentally understand how people can learn in effective, efficient, and enjoyable ways, and how you can teach and design learning materials to achieve this objective. If a learner doesn’t enjoy the learning experience, even if it’s effective and/or efficient, they won’t do it. The same is true for teaching: that is it must also be effective, efficient, and enjoyable for the teacher because if a teacher doesn’t enjoy the teaching process, even if it’s effective and/or efficient, they won’t do it.

Source: GUEST POST: An Interview With an Educational Realist and Grumpy Old Man — The Learning Scientists

Learning Curves, Given vs Generated Subgoal Labels, Replicating a US study in India, and Frames vs Text: More ICER 2016 Trip Reports

My Blog@CACM post for this month is a trip report on ICER 2016. I recommend Amy Ko’s excellent ICER 2016 trip report for another take on the conference. You can also see the Twitter live feed with hashtag #ICER2016.

I write in the Blog@CACM post about three papers (and reference two others), but I could easily write reports on a dozen more. The findings were that interesting and that well done. I’m going to give four more mini-summaries here, where the results are more confusing or surprising than those I included in the CACM Blog post.

This year was the first time we had a neck-and-neck race for the attendee-selected award, the “John Henry” award. The runner-up was Learning Curve Analysis for Programming: Which Concepts do Students Struggle With? by Kelly Rivers, Erik Harpstead, and Ken Koedinger. Tutoring systems can be used to track errors on knowledge concepts over multiple practice problems. Tutoring systems developers can show these lovely decreasing error curves as students get more practice, which clearly demonstrate learning. Kelly wanted to see if she could do that with open editing of code, not in a tutoring system. She tried to use AST graphs as a sense of programming “concepts,” and measure errors in use of the various constructs. It didn’t work, as Kelly explains in her paper. It was a nice example of an interesting and promising idea that didn’t pan out, but with careful explanation for the next try.

I mentioned in this blog previously that Briana Morrison and Lauren Margulieux had a replication study (see paper here), written with Adrienne Decker using participants from Adrienne’s institution. I hadn’t read the paper when I wrote that first blog post, and I was amazed by their results. Recall that they had this unexpected result where changing contexts for subgoal labeling worked better (i.e., led to better performance) for students than keeping students in the same context. The weird contextual-transfer problems that they’d seen previously went away in the second (follow-on) CS class — see below snap from their slides. The weird result was replicated in the first class at this new institution, so we know it’s not just one strange student population, and now we know that it’s a novice problem. That’s fascinating, but still doesn’t really explain why. Even more interesting was that when the context transfer issues go away, students did better when they were given subgoal labels than when they generated them. That’s not what happens in other fields. Why is CS different? It’s such an interesting trail that they’re exploring!

Mike Hewner and Shitanshu Mishra replicated Mike’s dissertation study about how students choose CS as a major, but in Indian institutions rather than in US institutions: When Everyone Knows CS is the Best Major: Decisions about CS in an Indian context. The results that came out of the Grounded Theory analysis were quite different! Mike had found that US students use enjoyment as a proxy for ability — “If I like CS, I must be good at it, so I’ll major in that.” But Indian students already thought CS was the best major. The social pressures were completely different. So, Indian students chose CS — if they had no other plans. CS was the default behavior.

One of the more surprising results was from Thomas W. Price, Neil C.C. Brown, Dragan Lipovac, Tiffany Barnes, and Michael Kölling, Evaluation of a Frame-based Programming Editor. They asked a group of middle school students in a short laboratory study (not the most optimal choice, but an acceptable starting place) to program in Java or in Stride, the new frame-based language and editing environment from the BlueJ/Greenfoot team.  They found no statistically significant differences between the two different languages, in terms of number of objectives completed, student frustration/satisfaction, or amount of time spent on the tasks. Yes, Java students got more syntax errors, but it didn’t seem to have a significant impact on performance or satisfaction. I found that totally unexpected. This is a result that cries out for more exploration and explanation.

There’s a lot more I could say, from Colleen Lewis’s terrific ideas to reduce the impact of CS stereotypes to a promising new method of expert heuristic evaluation of cognitive load.  I recommend reviewing the papers while they’re still free to download.

Preview ICER 2016: Ebooks Design-Based Research and Replications in Assessment and Cognitive Load Studies

The International Computing Education Research (ICER) Conference 2016 is September 8-12 in Melbourne, Australia (see website here). There were 102 papers submitted, and 26 papers accepted for a 25% acceptance rate. Georgia Tech computing education researchers are justifiably proud — we submitted three papers to ICER 2016, and we had three acceptances. We’re over 10% of all papers at ICER 2016.

One of the papers extends the ebook work that I’ve reported on here (see here where we made them available and our paper on usability and usage from WiPSCE 2015). Identifying Design Principles for CS Teacher Ebooks through Design-Based Research (click on the title to get to the ACM DL page) by Barbara Ericson, Kantwon Rogers, Miranda Parker, Briana Morrison, and I use a Design-Based Research perspective on our ebooks work. We describe our theory for the ebooks, then describe the iterations of what we designed, what happened when we deployed (data-driven), and how we then re-designed.

Two of our papers are replication studies — so grateful to the ICER reviewers and communities for seeing the value of replication studies. The first is Replication, Validation, and Use of a Language Independent CS1 Knowledge Assessment by Miranda Parker, me, and Shelly Engleman. This is Miranda’s paper expanding on her SIGCSE 2016 poster introducing the SCS1 validated and language-independent measure of CS1 knowledge. The paper does a great survey of validated measures of learning, explains her process, and then presents what one can and can’t claim with a validated instrument.

The second is Learning Loops: A Replication Study Illuminates Impact of HS Courses by Briana Morrison, Adrienne Decker, and Lauren Margulieux. Briana and Lauren have both now left Georgia Tech, but they were still here when they did this paper, so we’re claiming them. Readers of this blog may recall Briana and Lauren’s confusing results from SIGCSE 2016 result that suggest that cognitive load in CS textual programming is so high that it blows away our experimental instructional treatments. Was that an aberration? With Adrienne Decker’s help (and student participants), they replicated the study. I’ll give away the bottom line: It wasn’t an aberration. One new finding is that students who did not have high school CS classes caught up with those who did in the experiment, with respect to understanding loops

We’re sending three of our Human-Centered Computing PhD students to the ICER 2016 Doctoral Consortium. These folks will be in the DC on Sept 8, and will present posters to the conference on Sept 9 afternoon.

• Barbara Ericson will be presenting her results with Dynamically Adaptive Parsons Problems. I’ve seen some of the pilot study results from this summer, and they’re fascinating.
• Amber Solomon is just starting her second year working with me. She did the evaluation on the AR Design Studio classroom. She (and I) is fascinated by Steve Cooper’s results from ICER 2015 where spatial reasoning training influenced CS performance and reduced SES differences. She’s been doing a study on CS grades, SES, and spatial reasoning in a non-majors class. She’ll be presenting on The Role of Spatial Reasoning in Learning Computer Science.
• Kayla DesPortes works with my colleague Betsy DiSalvo on the learning that happens in MakerSpaces. She’s designing new kinds of physical interfaces to reduce cognitive load and improve learning when working with electronics, which she’ll be talking about at her poster: Learning and Collaboration in Physical Computing.

Seeking Collaborators for a Study of Achievement Goal Theory in CS1: Guest blog post by Daniel Zingaro

I have talked about Dan’s work here before, such as his 2014 award-winning ICER paper and his Peer Instruction in CS website. I met with Dan at the last SIGCSE where he told me about the study that he and Leo Porter were planning. Their results are fascinating since they are counter to what Achievement Goal Theory predicts. I invited him to write a guest blog post to seek collaborators for his study, and am grateful that he sent me this.

Why might we apply educational theory to our study of novice programmers? One core reason lies in theory-building: if someone has developed a general learning theory, then we might do well to co-opt and extend it for the computing context. What we get for free is clear: a theoretical basis, perhaps with associated experimental procedures, scales, hypotheses, and predictions. Unfortunately, however, there is often a cost in appropriating this theory: it may not replicate for us in the expected ways.

Briana Morrison’s recent work nicely highlights this point. In two studies, Briana reports her efforts to replicate what is known about subgoals and worked examples. Briefly, a worked example is a sample problem whose step-by-step solution is given to students. And subgoals are used to break that solution into logical chunks to hopefully help students map out the ways that the steps fit together to solve the problem.

Do subgoals help? Well, it’s supposed to go like this, from the educational psychology literature: having students generate their own labeled goals is best, giving students the subgoal labels is worse, and not using subgoals at all is worse still. But that isn’t what Briana found. For example, Briana reports [1] that, on Parsons puzzles, students who are given subgoal labels do better than both those who generate their own subgoal labels and those not given subgoals at all. Why the differences? One possibility is that programming exerts considerable cognitive load on the learner, and that the additional load incurred by generating subgoal labels overloads the student and harms learning.

The point here is that taking seriously the idea of leveraging existing theory requires concomitant attention to how and why the theory may operate differently in computing.

My particular interest here is in another theory from educational psychology: achievement goal theory (AGT). AGT studies the goals that students adopt in achievement situations, and the positive and negative consequences of those goals in terms of educationally-relevant outcomes. AGT zones in on two main goal types: mastery goals (where performance is defined intrapersonally) and performance goals (where performance is defined normatively in comparison to others).

Do these goals matter? Well, it’s supposed to go roughly like this: mastery goals are positively associated with many outcomes of value, such as interest, enjoyment, self-efficacy, and deep study strategies (but not academic performance); performance goals, surprisingly and confusingly, are positively associated with academic performance. But, paralleling the Briana studies from above, this isn’t what we’ve found in CS. With Leo Porter and my students, we’ve been studying goal-outcome links in novice CS students. We’ve found, contrary to theoretical expectations, that performance goals appear to be null or negative predictors of performance, and that mastery goals appear to be positive predictors of performance [2,3].

We are now conducting a larger study of achievement goals and outcomes of CS1 students — larger than that achievable with the couple of institutions to which we have access on our own. We are asking for your help.

The study involves administering two surveys to students in a CS1 course. The first survey, at the beginning of the semester, measures student achievement goals. The second survey, close to the end of the semester, measures potential mediating variables. We plan to collect exam grade, interest in CS, and other outcome variables.

The hope is that we can conduct a multi-institutional study of a variety of CS1 courses to strengthen what we know about achievement goals in CS.

Please contact me at daniel dot zingaro at utoronto dot ca if you are interested in participating in this work. Thanks!

[1] Briana Morrison. Subgoals Help Students Solve Parsons Problems. SIGCSE, 2016. ACM DL link.

[2] Daniel Zingaro. Examining Interest and Performance in Computer Science 1: A Study of Pedagogy and Achievement Goals. TOCE, 2015. ACM DL link.

[3] Daniel Zingaro and Leo Porter. Impact of Student Achievement Goals on CS1 Outcomes. SIGCSE, 2016. ACM DL link.

Are there elements of human nature that could be better harnessed for better educational outcomes?

I don’t often link to Quora, but when it’s Steven Pinker pointing out the relationship between our human nature to educational goals, it’s worth it.

One potential insight is that educators begin not with blank slates but with minds that are adapted to think and reason in ways that may be at cross-purposes with the goals of education in a modern society. The conscious portion of language consists of words and meanings, but the portion that connects most directly to print consists of phonemes, which ordinarily are below the level of consciousness. We intuitively understand living species as having essences, but the theory of evolution requires us to rethink them as populations of variable individuals. We naturally assess probability by dredging up examples from memory, whereas real probability takes into account the number of occurrences and the number of opportunities. We are apt to think that people who disagree with us are stupid and stubborn, while we are overconfident and self-deluded about our own competence and honesty.

Source: (3) Are there elements of human nature that could be better harnessed for better educational outcomes? – Quora

Why Students Don’t Like Active Learning: Stop making me work at learning!

I enjoy reading Annie Murphy Paul’s essays, and this one particularly struck home because I just got my student opinion surveys from last semester.  I use active learning methods in my Media Computation class every day, where I require students to work with one another. One student wrote:

“I didn’t like how he forced us to interact with each other. I don’t think that is the best way for me to learn, but it was forced upon me.”

It’s true. I am a Peer Instruction bully.

At a deeper level, it’s amazing how easily we fool ourselves about what we learn from and what we don’t learn from.  It’s like the brain training work.  We’re convinced that we’re learning from it, even if we’re not. This student is convinced that he doesn’t learn from it, even though the available evidence says she or he does.

In case you’re wondering about just what “active learning” is, here’s a widely-accepted definition: “Active learning engages students in the process of learning through activities and/or discussion in class, as opposed to passively listening to an expert. It emphasizes higher-order thinking and often involves group work.”

Source: Why Students Don’t Like Active Learning « Annie Murphy Paul

Transfer of learning: Making sense of what education research is telling us

I enjoy reading “Gas station without pumps,” and the below-quoted post was one I wanted to respond to.

Two of the popular memes of education researchers, “transferability is an illusion” and “the growth mindset”, are almost in direct opposition, and I don’t know how to reconcile them.

One possibility is that few students actually attempt to learn the general problem-solving skills that math, CS, and engineering design are rich domains for.  Most are content to learn one tiny skill at a time, in complete isolation from other skills and ideas. Students who are particularly good at memory work often choose this route, memorizing pages of trigonometric identities, for example, rather than learning how to derive them at need from a few basics. If students don’t make an attempt to learn transferable skills, then they probably won’t.  This is roughly equivalent to claiming that most students have a fixed mindset with respect to transferable skills, and suggests that transferability is possible, even if it is not currently being learned.

Teaching and testing techniques are often designed to foster an isolation of ideas, focusing on one idea at a time to reduce student confusion. Unfortunately, transferable learning comes not from practice of ideas in isolation, but from learning to retrieve and combine ideas—from doing multi-step problems that are not scaffolded by the teacher.

Source: Transfer of learning | Gas station without pumps

The problem with “transferability” is that it’s an ill-defined term.  Certainly, there is transfer of skill between domains.  Sharon Carver showed a long time ago that she could teach debugging Logo programs, and students would transfer that debugging process to instructions on a map (mentioned in post here).  That’s transferring a skill or a procedure.  We probably do transfer big, high-level heuristics like “divide-and-conquer” or “isolate the problem.”  One issue is whether we can teach them.  John Sweller says that we can’t — we must learn them (it’s a necessary survival skill), but they’re learned from abstracting experience (see Neil Brown’s nice summary of Sweller’s SIGCSE keynote).

Whether we can teach them or not, what we do know is that higher-order thinking is built on lots of content knowledge. Novices are unlikely to transfer until they know a lot of stuff, a lot of examples, a lot of situations. For example, novice designers often have “design fixation.”  They decide that the first thing they think of must be the right answer.  We can insist that novice designers generate more designs, but they’re not going to generate more good designs until they know more designs.  Transfer happens pretty easily when you know a lot of content and have seen a lot of situations, and you recognize that one situation is actually like another.

Everybody starts out learning one tiny skill at a time.  If you know a lot of skills (maybe because you have lots of prior experience, maybe because you have thought about these skills a lot and have recognized the general principles), you can start chunking these skills and learning whole schema and higher-level skills.  But you can’t do that until you know lots of skills.  Students who want to learn one tiny skill at a time may actually need to still learn one tiny skill at a time. People abstract (e.g., able to derive a solution rather than memorize it) when they know enough content that it’s useful and possible for them to abstract over it.  I completely agree that students have to try to abstract.  They have to learn a lot of stuff, and then they have to be in a situation where it’s useful for them to abstract.

“Growth mindset” is a necessity for any of this to work.  Students have to believe that content is worth knowing and that they can learn it.  If students believe that content is useless, or that they just “don’t do math” or “am not a computer person” (both of which I’ve heard in just the last week), they are unlikely to learn content, they are unlikely to see patterns in it, and they are unlikely to abstract over it.

Kevin is probably right that we don’t teach problem solving in engineering or computing well.  I blogged on this theme for CACM last month — laboratory experiments work better for a wider range students than classroom studies.  Maybe we teach better in labs than in classrooms?  The worked examples effect suggests that we may be asking students to problem solve too much.  We should show students more completely worked out problems.  As Sweller said at SIGCSE, we can’t expect students to solve novel problems.  We have to expect students to match new problems to solutions that they have already seen.  We do want students to solve problems, too, and not just review example solutions. Trafton and Reiser showed that these should be interleaved: Example, Problem, Example, Problem… (see this page for a summary of some of the worked examples research, including Trafton & Reiser).

When I used to do Engineering Education research, one of my largest projects was a complete flop.  We had all this prior work showing the benefits of a particular collaborative learning technology and technique, then we took it into the engineering classroom and…poof! Nothing happened.  In response, we started a project to figure out why it failed so badly.  One of our findings was that “learned helplessness” was rampant in our classes, which is a symptom of a fixed mindset.  “I know that I’m wrong, and there’s nothing that I can do about it.  Collaboration just puts my errors on display for everyone,” was the kind of response we’ve got. (See here for one of our papers on this work.)

I believe that all the things Kevin sees going wrong in his classes really are happening.  I believe he’s not seeing transfer that he might reasonably expect to see.  I believe that he doesn’t see students trying to abstract across lower-level skills.  But I suspect that the problem is the lack of a growth mindset.  In our work, we saw Engineering students simply give up.  They felt like they couldn’t learn, they couldn’t keep up, so they just memorized.  I don’t know that that’s the cause of the problems that Kevin is seeing.  In my work, I’ve often found that motivation and incentive are key to engagement and learning.